在之前的BLOG里，我们一同了解了神经网络的一些数学记号和表示方法。现在就让我们通过实例了解神经网络在非线性假设函数，特别是逻辑运算假设函数的运用吧！

逻辑运算假设函数

我们考虑下面的问题，我们有二进制的输入特征 x1 x2 ，其要么取0 要么取1 ，在这个例子中只画出了两个正样本和 两个负样本：

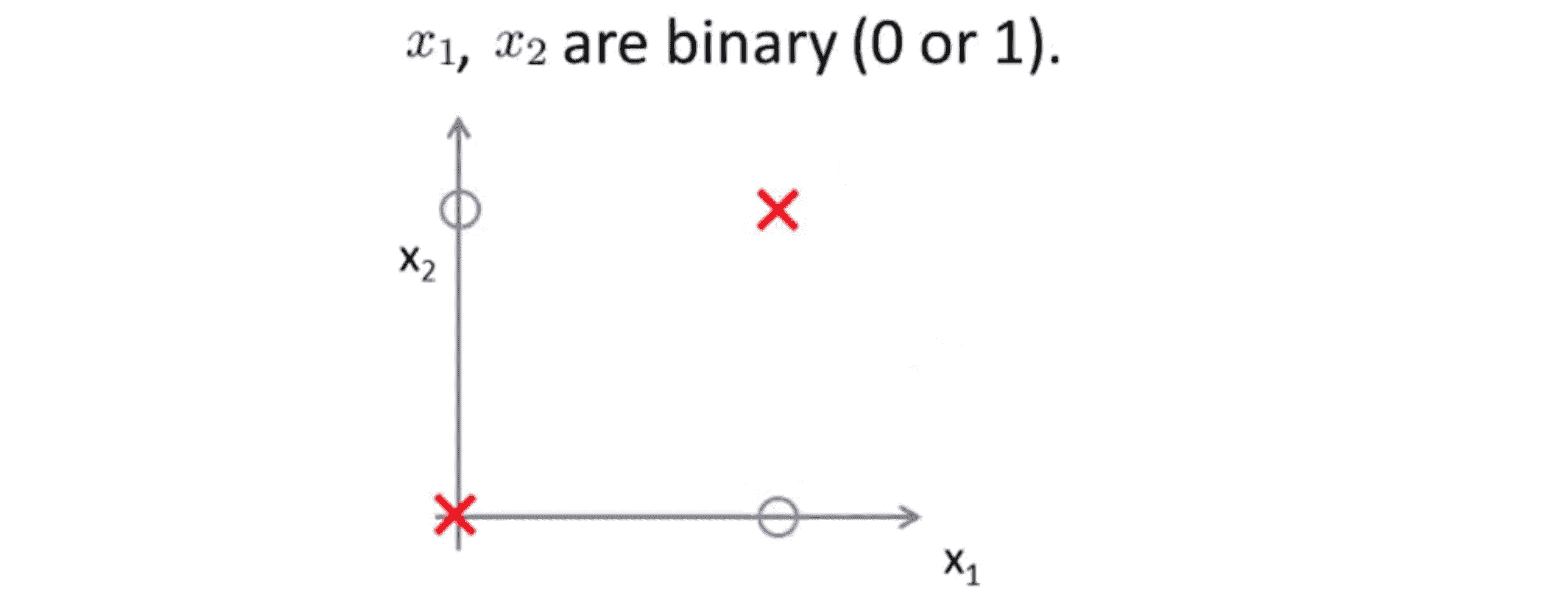
但我们可以认为这是一个更复杂的学习问题的简化版本，在这个复杂问题中，我们可能在右上角和左下角有一堆正样本 ，其余地方负样本：

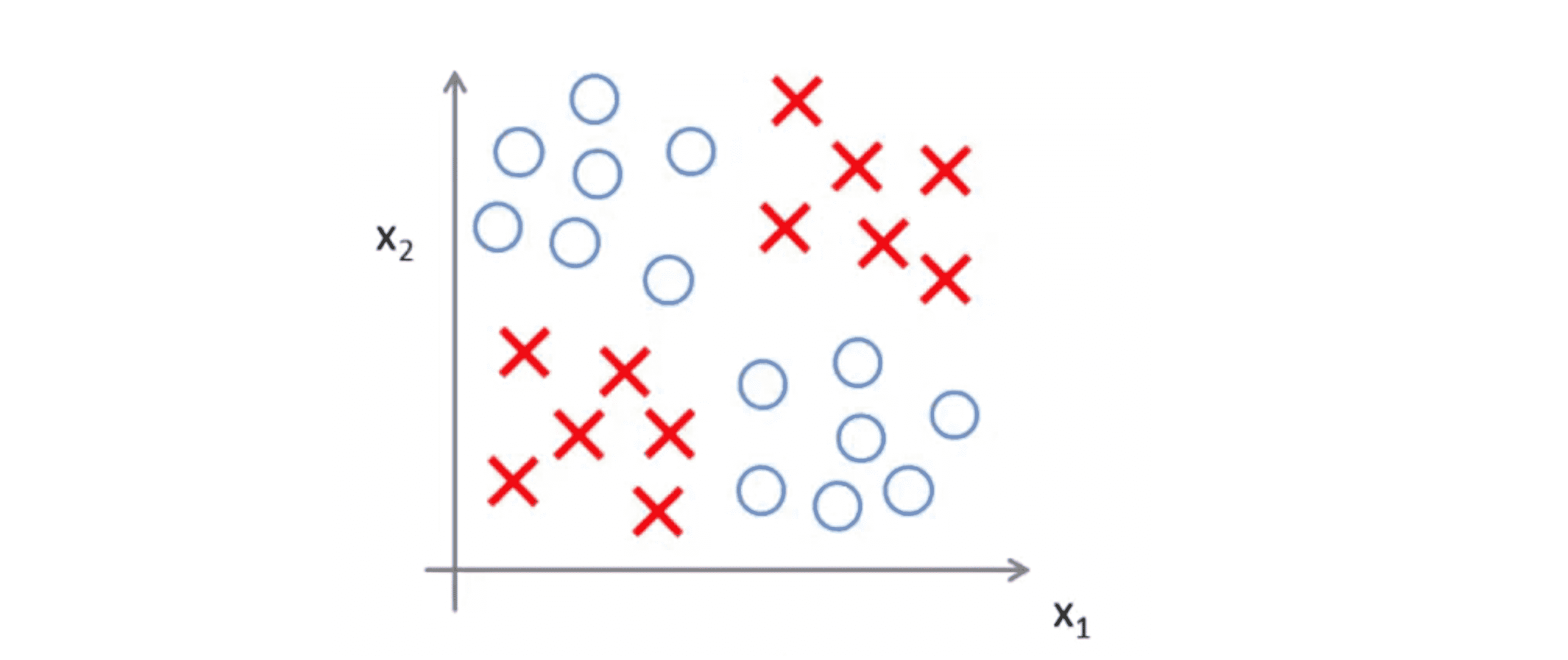
我们想要学习一种非线性的决策边界来区分正负样本，大概可能得到下面这样：

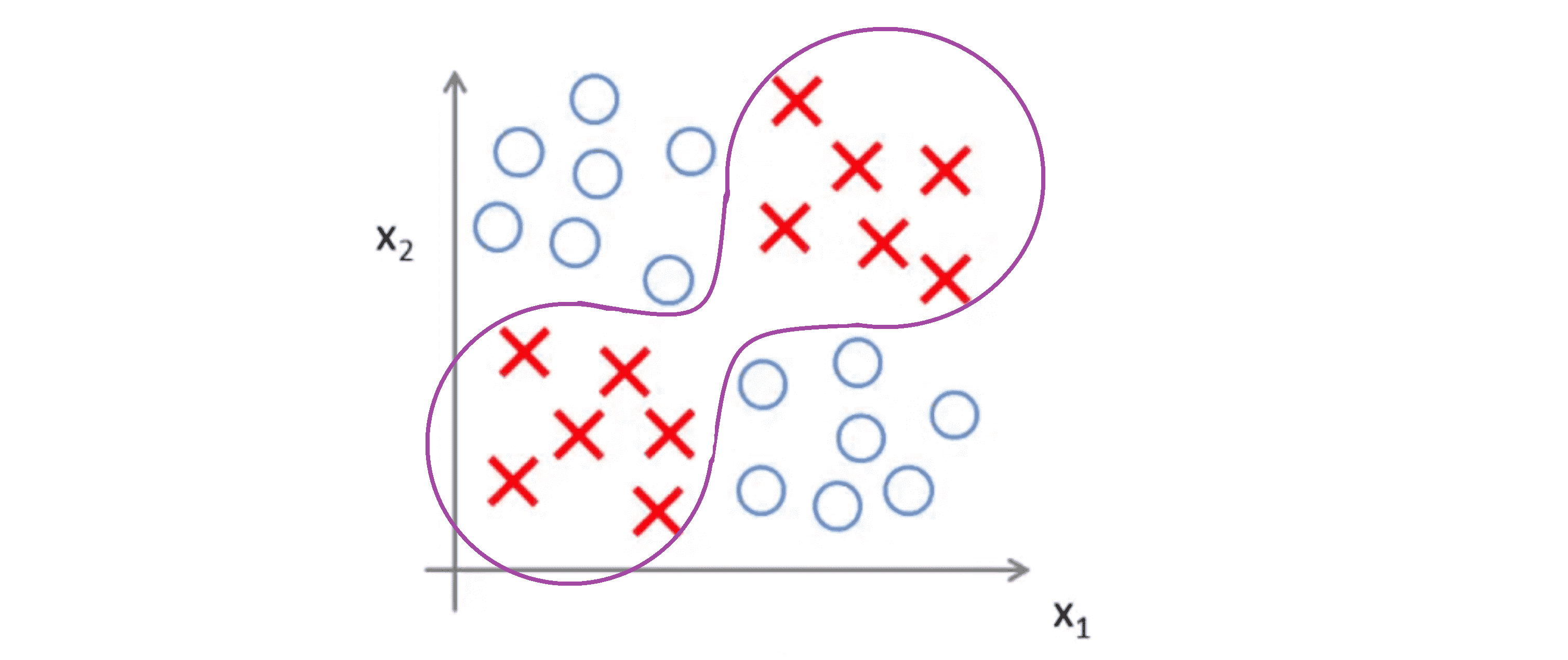
那么神经网络是如何做到的呢？为了讲解方便下面我不用复杂版的例子，改用最前面的简单版的例子，这样更容易说明。具体来讲这里需要计算的是目标函数 y = x1 XOR x2 或者 y = x1 NXOR x2 。其中异或非(NXOR)表示 x1 异或(XOR) x2 后取反。顺带一提，异或是逻辑运算的一种， x1 异或 x2 为真当且仅当 x1 与 x2 中有且仅有一个为 1 。，接下来我们以 NXOR 为例子，我们想要知道是否能找到一个神经网络模型来拟合这种训练集，为了建立能拟合 XNOR 运算的神经网络，我们先看看如何建立其他更简单的逻辑运算的神经网络。

与运算假设函数

我们先看一个稍微简单的神经网络，它拟合了“与运算” ，即假设我们输入 x1 和 x2 并且都是二进制，我们的目标 函数 y = x1 & x2 。与运算也是逻辑运算的一种，其值为 1 当且仅当 x1 = x2 = 1。那我们怎样得到一个具有单个神经元的神经网络来计算这个逻辑运算与呢?

为了做到这一点，我们也需要有个偏置单元 x0，其值恒等于 1 .现在我们给下图这个网络分配一些权重：

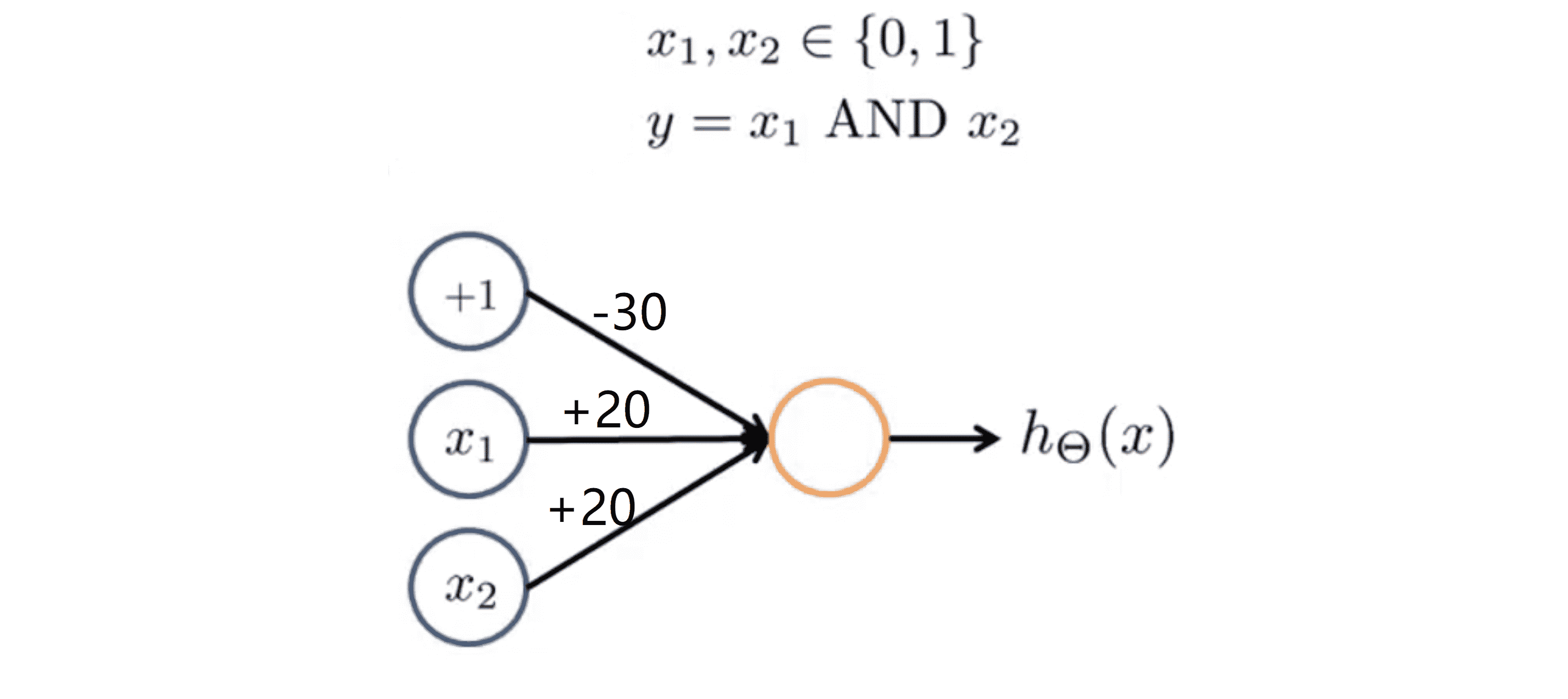
所以我的假设ħ(x) = g(-30 + 20 * x1 + 20 * x2)。其实我们知道在这幅神经网络图中 -30 其实是 Θ(1)10，第一个 20 是 Θ(1)11 ，第二个 20 是 Θ(1)12。让我们来看看这个小神经元是怎样计算的。

我们的g(z)其实是 s 型函数。回忆一下我们的 s 型激励函数 g(z) 看起来是下图这样的：

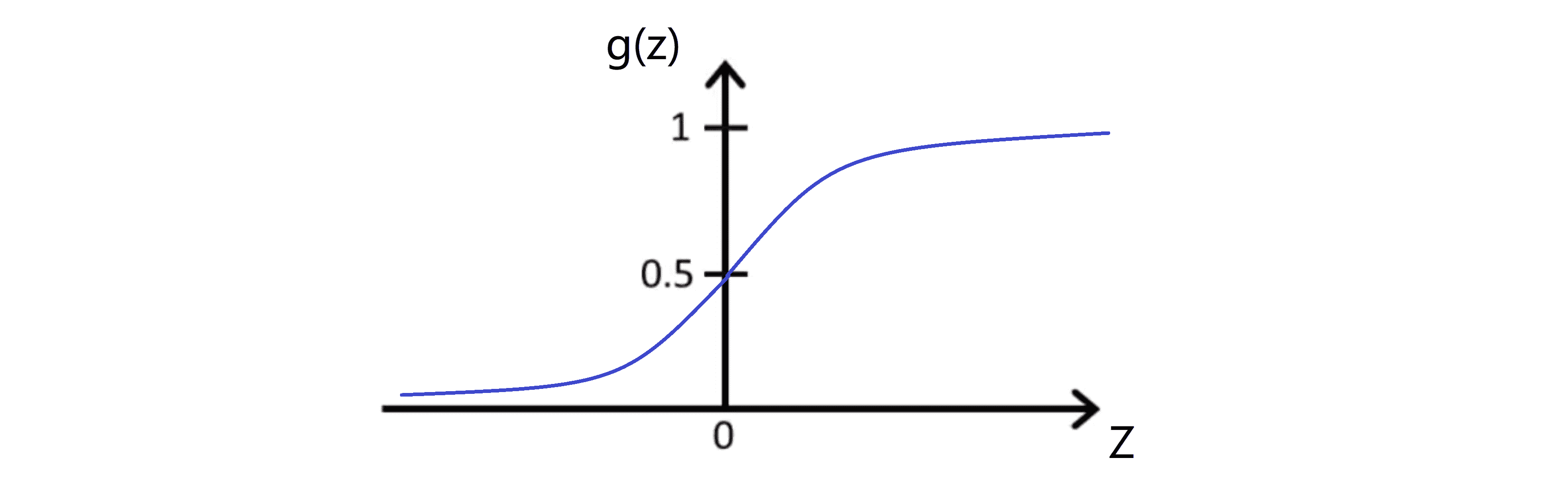
它的函数值从 0 开始上升，穿过 0.5 后渐进到1。其实它渐进的很快，如果横轴值 z 等于4.6 ，则S形函数等于0.99 ，这是非常接近 1 的。并且由于对称性，如果 z为 -4.6，S 形函数的值就等于0.01，也非常接近0。

让我们来看看四种可能的输入值， x1 和 x2 都只可能取 0 或 1，所以一共只有四种可能输入(0, 0), (0, 1), (1, 0), (1, 1)，我们分别进行计算得到下图：

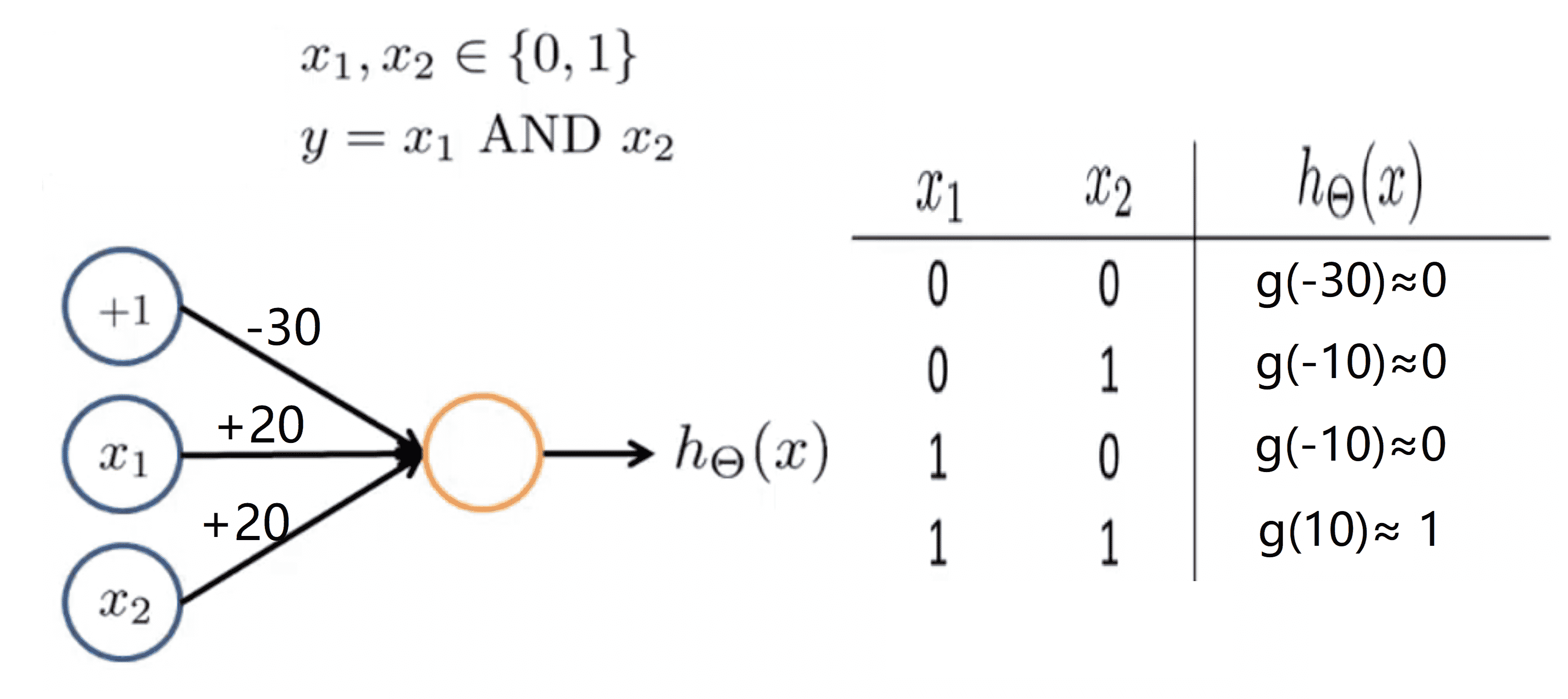
让我们一个个看如果 x1 和 x2 均为 0 ，那么g(-30 + 20 * x1 + 20 * x2) = g(-30)， g(-30)在之前那副图的很左边的地方，所以其值非常接近于 0 ；接下来，如果x1 等于 0 且 x2 等于 1 ，那么g(-30 + 20 * x1 + 20 * x2) = g(-10) 也在很左边的位置，所以其值也是非常接近 0 。如果 x1 等于 1 并且 x2等于 0 的话，我们也同样有g(-30 + 20 * x1 + 20 * x2) = g(-10) 也在很左边的位置，所以其值也是非常接近 0 。最后如果 x1 等于 1 且 x2 等于 1 ，那么g(-30 + 20 * x1 + 20 * x2) = g(10)，其值是非常接近 1 的。如果你认真看看我们得出的上图右边的表格，其实这就是逻辑“与”的计算结果，换句话说，我们得到的假设输出 1 当且仅当 x1 x2 都等于 1 。所以这里我们通过一个单元的神经网络实现了与“与”运算相似的结果。

或运算

下面我们要介绍的神经网络实现了或运算函数的功能。或运算也是逻辑运算的一种，也就是x1 | x2，其值为 1 只需要 x1 和 x2 中至少有一个为 1 就可以了，接下来我们来看看是如何实现的。其实还是单神经元的神经网络，只不过权重发生了改变，变成了下图这样：

如果我们把假设函数写出来，其就为ħ(x) = g(-10 + 20 * x1 + 20 * x2)。同样地，x1 和 x2 都只可能取 0 或 1，所以一共只有四种可能输入(0, 0), (0, 1), (1, 0), (1, 1)，我们分别进行计算得到下图：

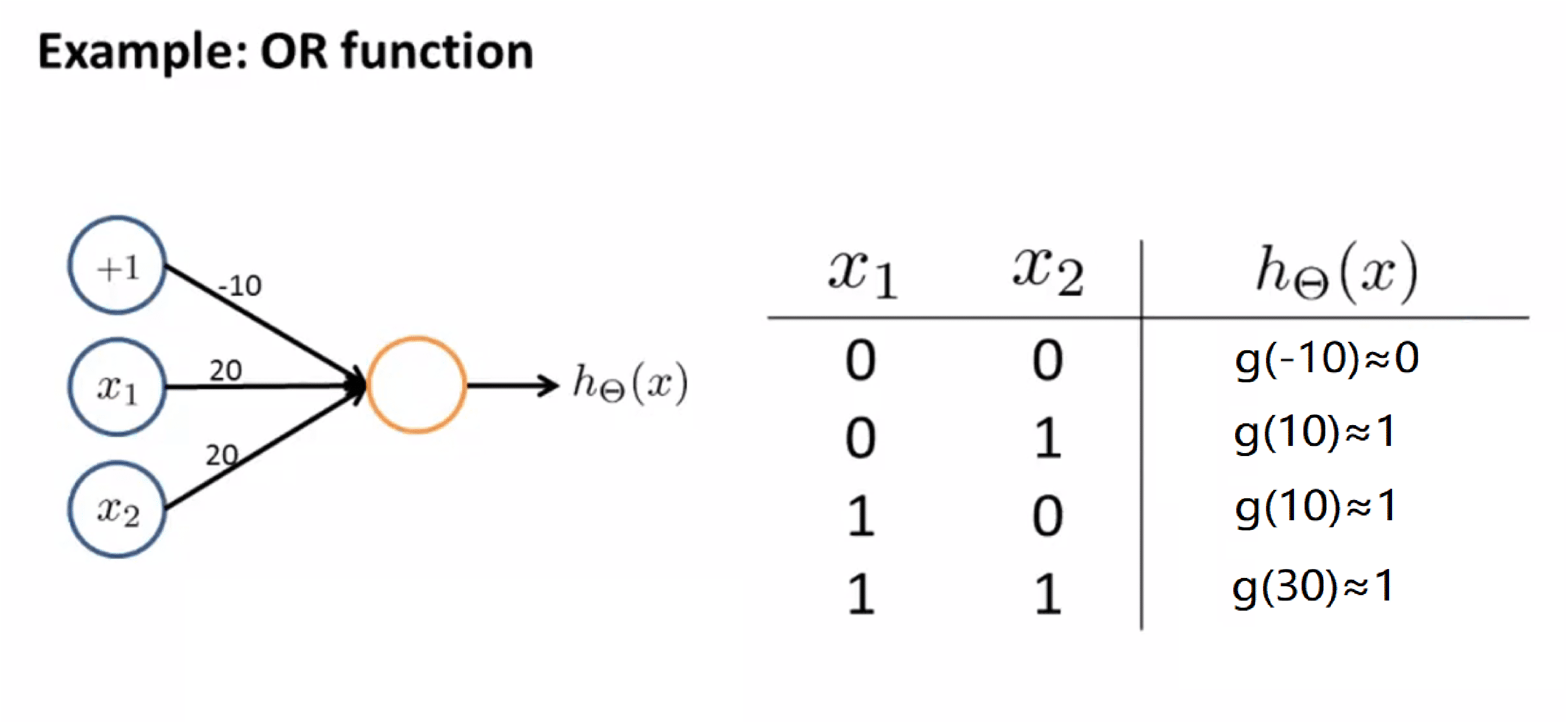
计算过程和与运算的那个相似，这里就不赘述了。所以我们发现，我们的计算结果本质上就是逻辑或运算得到的值。我们也仅仅使用了一个神经元就完成了逻辑"或"的运算。

非运算

接下来我们来看看逻辑非运算，也就是计算 "!x" ,非运算也是逻辑运算的一种，其值为 1 当且仅当 x = 0。下面我们来看看具体是如何实现的。

我们先画出这个神经网络中的神经元和相连接的各权值:

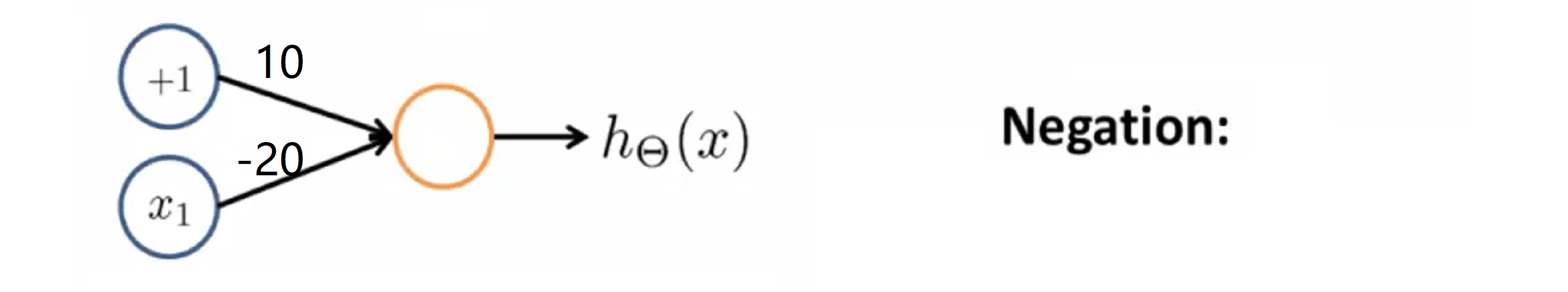
这里我们只有一个输入量 x1 ，在这里我们也加上了表示偏差的单位元的 +1 。如果我将输入单元和两个权数相连，也就是+10和-20，则可用以下假设方程来计算 h(x) = g(10 - 20 * x1) 。同样地，其中 g 是一个 S 型函数。，我们同样讨论 x1 取 0 还是 1， 计算如下：

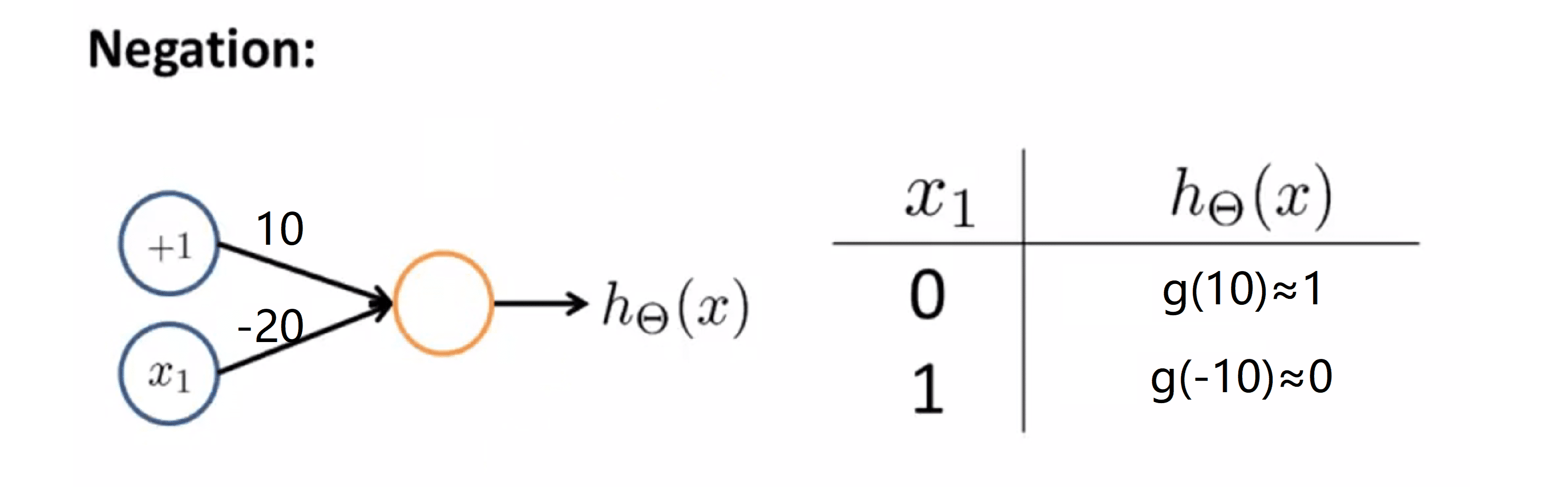
当x1等于0时，计算出假设函数 g(10 - 20 * x1) = g(10)， 这个值近似的等于 1 ；而当 x 等于 1 时，计算出的假设函数 g(10 - 20 * x1) = g(-10)，也就是约等于 0。如果我们观察这两个值，就发现这实际上计算的 就是"!x1"函数。所以要计算逻辑非运算总体思路就是在我们所希望取非运算的变量前面放上一个绝对值大的负数作为权值，因此如果放一个 -20 和 x1 相乘，很显然最终的结果就得到了对 x1 进行非运算的效果。

同样的， (!x1) & (!x2) 也大概应该知道至少应该在x1和x2前面放一个绝对值比较大的负数作为权值。现在你应该也清楚了怎样建立一个小规模的神经网络来计算这些简单的逻辑函数的值。

亦或运算

把以上我们介绍的这三个部分内容放在一起 x1 & x2 与 (!x1) & (!x2) 与 x1 | x2的三个神经网络放在一起：

现在我们就有足够的工具去计算 x1 XNOR x2了。 首先，我们需要输入单元 +1，x1 和 x2，然后建立第一个隐藏层单元我们称其为 a(2)1 ，接下来我要从红色的网络，也就是x1 & x2这个网络复制出权值，也就是-30 20 20。 接下来我再建立第二个隐藏单元，我们称之为a(2)2，然后再从中间的蓝色的网络中复制出权值，也就是(!x1) & (!x2)，这样我们就有了 10 -20 -20 这样三个权值。最后我们建立输出节点，也就是输出单元 a(3)1，这也是等于输出值h(x) ，然后复制一个或运算网络，同时我们需要一个 +1 作为偏差单元，也将其添加进来，然后从绿色的网络中复制出所有的权值，即x1 | x2，也就是-10 20 20 得到我们的完整网络：

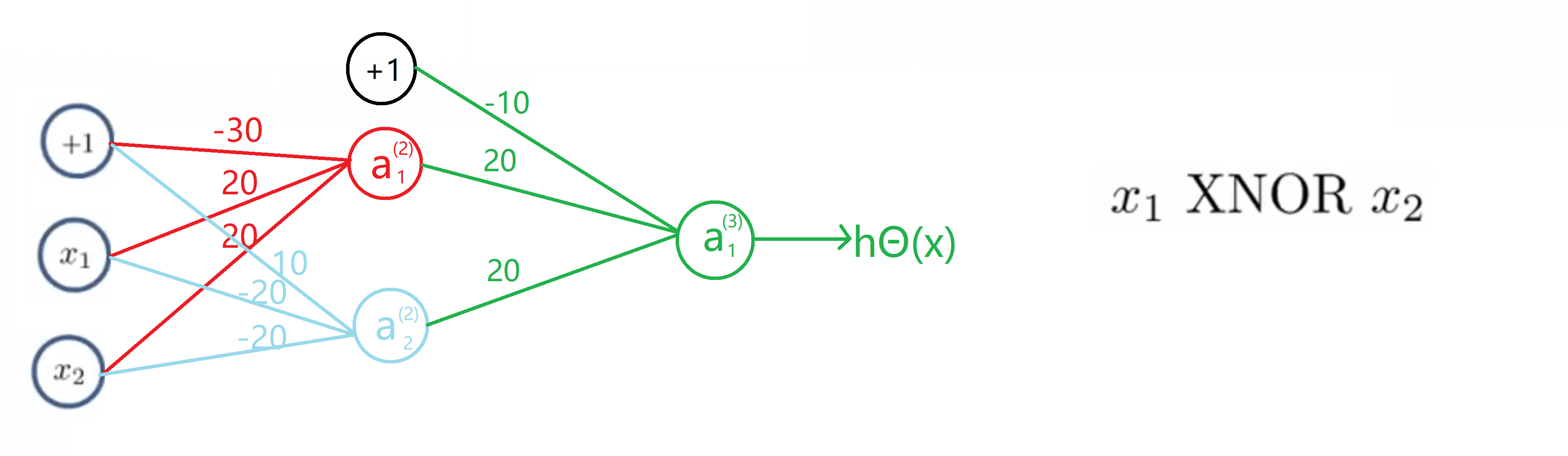
我们来计算一下真值表中的值，对于a (2)1，也就是红色的网络我们知道是 x1 和 x2 的与运算，所以得到的值等于0 0 0 1，这取决于 x1 和 x2 的具体取值。对于a (2)2 也就是蓝色的网络，我们知道这是(非x1)与(非x2)的运算，那么对于 x1 和 x2 的四种取值，其结果将为 1 0 0 0。 然后我们继续看真值表的值，对于a (3)1， 第一行的值是 0 和 1 的或运算，其结果为1，然后是 0 和 0 的或运算， 其结果为 0，接着还是 0 和 0 的或运算，结果还是0，最后是 1 和 0 的或运算，其结果为1：

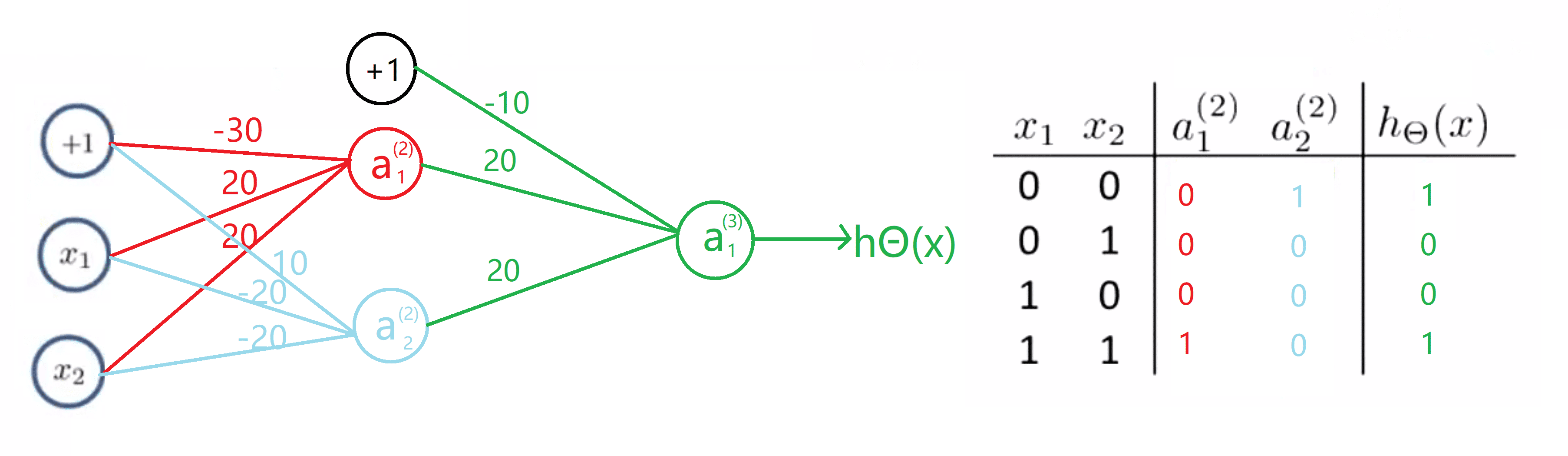
因此 h(x) 的值等于 1 当且仅当 x1 和 x2 都为 0 或者 x1 和 x2 都为 1 的时候。具体来说，在这两种情况下，h(x)输出 1。 在另两种情况下， h(x) 输出0。那么对于这样一个神经网络，我们有一个输入层，一个隐藏层和一个输出层。我们最终得到了计算 XNOR 函数的非线性判别边界。

更一般的理解是如下图：

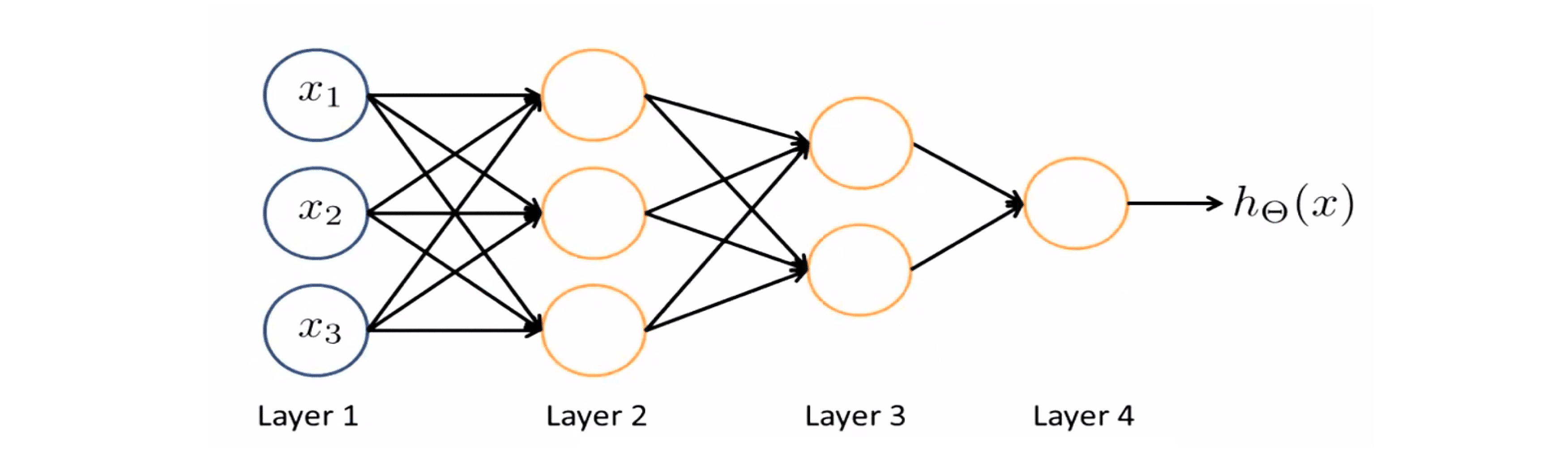
在输入层中，我们只有原始输入值；然后我们建立了一个隐藏层用来计算稍微复杂一些的输入量的函数; 如图所示 这些都是稍微复杂一些的函数；然后通过再添加另一个隐藏层，我们又得到了一个更复杂一点的函数……这就是关于神经网络可以计算较复杂函数的某种直观解释。

我们知道当层数很多的时候，你有一个相对简单的输入量的函数，我们可以在第二层、第三层建立的基础上，计算更加复杂一些的函数，然后再继续下一层，又可以计算再复杂一些的函数……这就是神经网络原理的直观理解。

结语

通过这篇BLOG，相信你已经对小型神经网络的搭建有了一些自己的理解和看法。接下来的BLOG，我们会看一看神经网络又是如何解决多元分类的。最后希望你喜欢这篇BLOG！