我们都知道,一种波长的可见光会对应一种固定的颜色。你是否会好奇,波长为X的可见光所对应的颜色的RGB值为多少呢?这篇博客就是要告诉你如何实现光的波长和RGB值的转换。
原理部分
说到波长与颜色的转换,第一反应便是色度图,而我采用的就是1931CIE-XYZ标准色度系统。
所谓1931CIE-XYZ系统,就是在RGB系统的基础上,用数学方法,选用三个理想的原色来代替实际的三原色,从而将CIE-RGB系统中的光谱三刺激值 和色度坐标r、g、b均变为正值。
下面我们来介绍一下CIE-RGB系统与CIE-XYZ系统的转换关系。选择三个理想的原色(三刺激值)X、Y、Z,X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色,而是虚构的假想色。它们在色度图中的色度坐标分别为:
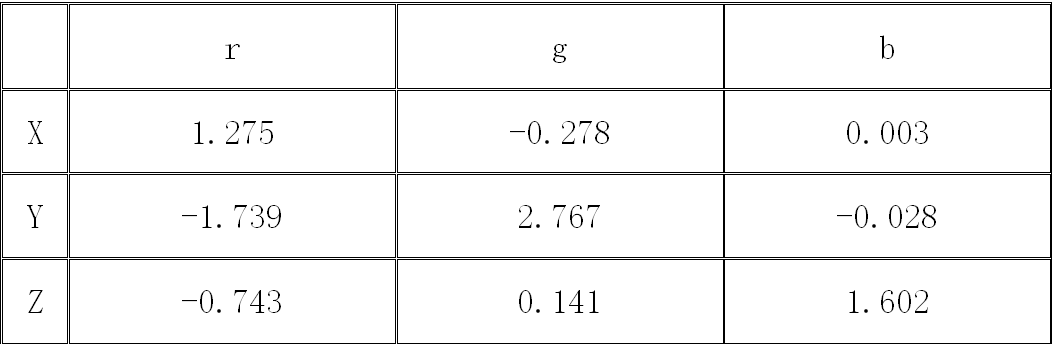
从下图中可以看到虚线三角形将整个光谱轨迹包含在内。因此整个光谱色变成了以XYZ三角形作为色域的域内色。在XYZ系统中所得到的光谱三刺激值x(γ)、y(γ) 、z(γ)、和色度坐标x、y、z将完全变成正值。经数学变换,两组颜色空间的三刺激值有以下关系:
X=0.490R+0.310G+0.200B
Y=0.177R+0.812G+0.011B
Z= 0.010G+0.990B
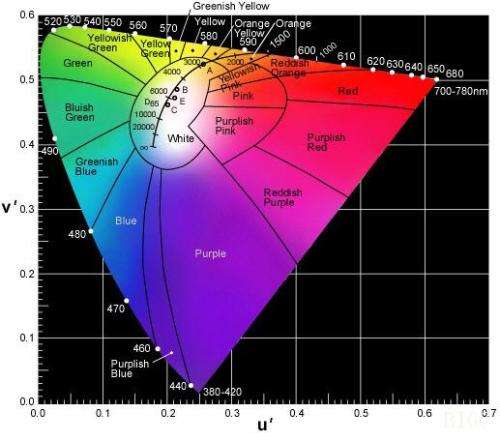
经过数学公式的推演和反推,我们得到两组颜色空间色度坐标的相互转换关系为:
x=(0.490r+0.310g+0.200b)/(0.667r+1.132g+1.200b)
y=(0.117r+0.812g+0.010b)/(0.667r+1.132g+1.200b)
z=(0.000r+0.010g+0.990b)/(0.667r+1.132g+1.200b)
这就是我们通常用来进行变换的关系式,所以,只要知道某一颜色的色度坐标r、g、b,即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。通过式的变换,对光谱色或一切自然界的色彩而言,变换后的色度坐标均为正值,而且等能白光的色度坐标仍然是(0.33,0.33),没有改变。
同理,经过数学的计算,也能得出光的波长与三原色XYZ颜色空间的的色度坐标x、y、z的相互转换,其大致表格如下:

也就是说我们要做的是通过算法把光的波长转换为色度坐标x、y、z,再把色度坐标转化为该波长所对应的可见光的R,G,B值。
至此,我们就已经完成了光的波长到R,G,B值的理论转化,接下来我就介绍一下我的程序算法。
程序部分
首先,我们要做的是把波长转化为所对应的X,Y,Z值,在这里为了尽可能快速的计算完成,我们采用了打表的以空间换取时间的高效算法,在这种算法的条件下,我们可以轻松的做到在O(1)的时间复杂度下计算长转化为所对应的X,Y,Z值。
其次,我们需要对X,Y,Z值进行数学操作,使其转化为对应的RGB值。在这里我们只需要将X,Y,Z值代入两组颜色空间色度坐标的相互转换关系,运用高斯消元的方法解出方程组的解即可。
但是我们发现,这只是关于R,G,B三个值的方程,使用高斯消元固然可以,但有些大材小用,所以在这里,我们也可运用暴力枚举R,G,B值的方式找到方程的解,具体代码如下:
xx=x[b];yy=y[b];zz=z[b];mi=32768;
for(int i=0;i<=255;i++)
for(int j=0;j<=255;j++)
for(int k=0;k<=255;k++)
{
if(i+k+j>0)
{
rr=0.490*i+0.310*j+0.200*k;
rr=rr/(0.667*i+1.132*j+1.200*k);
gg=0.117*i+0.812*j+0.010*k;
gg=gg/(0.667*i+1.132*j+1.200*k);
bb=0.000*i+0.010*j+0.990*k;
bb=bb/(0.667*i+1.132*j+1.200*k);
m=(rr-xx)*(rr-xx)+(gg-yy)*(gg-yy)+(bb-zz)*(bb-zz);
if(m<mi)
{
mi=m;
rrr=i;
ggg=j;
bbb=k;
}
}
}其中的rrr,ggg,bbb就是我们要求解的R,G,B值。
接着我们的问题就是如何用c++输出一组R,G,B对应的颜色的图像?这里我们给出模板,其中a[i][j][0] a[i][j][1] a[i][j][2] 分别代表第i行第j列的像素点所对应的R,G,B值,所以总的模板如下:
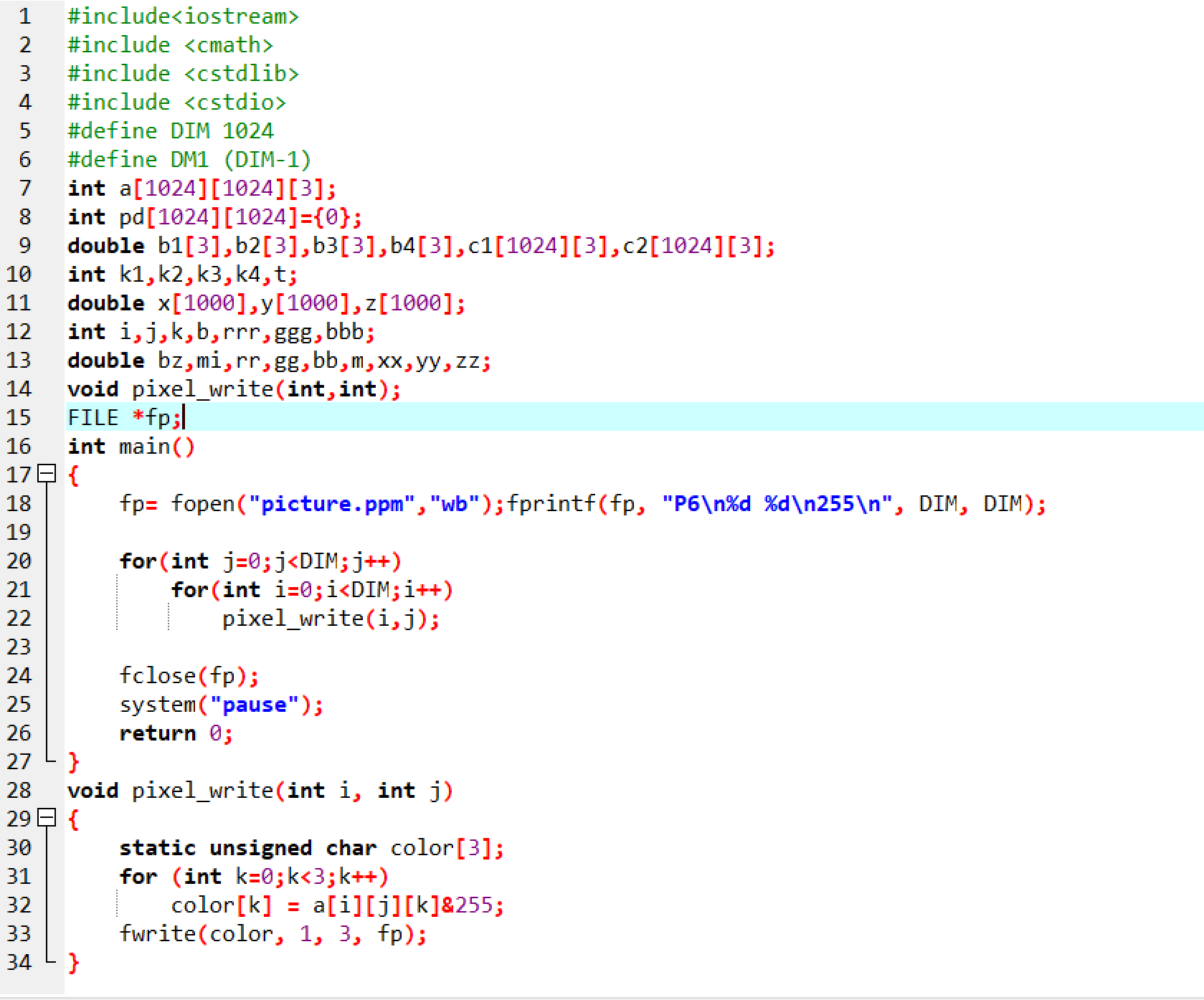
总的程序如下:
#include<iostream>
#include <cmath>
#include <cstdlib>
#include <cstdio>
#define DIM 1024
#define DM1 (DIM-1)
int a[1024][1024][3];
int pd[1024][1024]={0};
double b1[3],b2[3],b3[3],b4[3],c1[1024][3],c2[1024][3];
int k1,k2,k3,k4,t;
double x[1000],y[1000],z[1000];
int i,j,k,b,rrr,ggg,bbb;
double bz,mi,rr,gg,bb,m,xx,yy,zz;
void pixel_write(int,int);
FILE *fp;
int main()
{
fp= fopen("picture.ppm","wb");fprintf(fp, "P6\n%d %d\n255\n", DIM, DIM);
a[0][0][0]=0;a[0][0][1]=0;a[0][0][2]=0;
while(true)
{
printf("请输入波长(nm):");
scanf("%lf",&bz);
if(bz>=380 && bz<=780)break;
printf("这不是可见光哦,再输入一次吧\n");
}
b=int(bz);k=b%5;
if(k>=3)b=b+5-k;
else b=b-k;
x[380]=0.1741;y[380]=0.0050;z[380]=0.8209;
x[385]=0.1740;y[385]=0.0050;z[385]=0.8210;
x[390]=0.1738;y[390]=0.0049;z[390]=0.8213;
x[395]=0.1736;y[395]=0.0049;z[395]=0.8215;
x[400]=0.1733;y[400]=0.0048;z[400]=0.8219;
x[405]=0.1730;y[405]=0.0048;z[405]=0.8222;
x[410]=0.1726;y[410]=0.0048;z[410]=0.8226;
x[415]=0.1721;y[415]=0.0048;z[415]=0.8231;
x[420]=0.1714;y[420]=0.0051;z[420]=0.8235;
x[425]=0.1703;y[425]=0.0058;z[425]=0.8239;
x[430]=0.1689;y[430]=0.0069;z[430]=0.8242;
x[435]=0.1669;y[435]=0.0086;z[435]=0.8245;
x[440]=0.1644;y[440]=0.0109;z[440]=0.8247;
x[445]=0.1611;y[445]=0.0138;z[445]=0.8251;
x[450]=0.1566;y[450]=0.0177;z[450]=0.8257;
x[455]=0.1510;y[455]=0.0227;z[455]=0.8263;
x[460]=0.1440;y[460]=0.0297;z[460]=0.8263;
x[465]=0.1355;y[465]=0.0399;z[465]=0.8246;
x[470]=0.1241;y[470]=0.0578;z[470]=0.8181;
x[475]=0.1096;y[475]=0.0868;z[475]=0.8036;
x[480]=0.0913;y[480]=0.1327;z[480]=0.7760;
x[485]=0.0687;y[485]=0.2007;z[485]=0.7306;
x[490]=0.0454;y[490]=0.2950;z[490]=0.6596;
x[495]=0.0235;y[495]=0.4127;z[495]=0.5638;
x[500]=0.0082;y[500]=0.5384;z[500]=0.4534;
x[505]=0.0039;y[505]=0.6548;z[505]=0.3413;
x[510]=0.0139;y[510]=0.7502;z[510]=0.2359;
x[515]=0.0389;y[515]=0.8120;z[515]=0.1491;
x[520]=0.0743;y[520]=0.8338;z[520]=0.0919;
x[525]=0.1142;y[525]=0.8262;z[525]=0.0596;
x[530]=0.1547;y[530]=0.8059;z[530]=0.0394;
x[535]=0.1929;y[535]=0.7816;z[535]=0.0255;
x[540]=0.2296;y[540]=0.7543;z[540]=0.0161;
x[545]=0.2658;y[545]=0.7243;z[545]=0.0099;
x[550]=0.3016;y[550]=0.6923;z[550]=0.0061;
x[555]=0.3373;y[555]=0.6589;z[555]=0.0038;
x[560]=0.3731;y[560]=0.6245;z[560]=0.0024;
x[565]=0.4087;y[565]=0.5896;z[565]=0.0017;
x[570]=0.4441;y[570]=0.5547;z[570]=0.0012;
x[575]=0.4788;y[575]=0.5202;z[575]=0.0010;
x[580]=0.5125;y[580]=0.4866;z[580]=0.0009;
x[585]=0.5448;y[585]=0.4544;z[585]=0.0008;
x[590]=0.5752;y[590]=0.4242;z[590]=0.0006;
x[595]=0.6029;y[595]=0.3965;z[595]=0.0006;
x[600]=0.6270;y[600]=0.3725;z[600]=0.0005;
x[605]=0.6482;y[605]=0.3514;z[605]=0.0004;
x[610]=0.6658;y[610]=0.3340;z[610]=0.0002;
x[615]=0.6801;y[615]=0.3197;z[615]=0.0002;
x[620]=0.6915;y[620]=0.3083;z[620]=0.0002;
x[625]=0.7006;y[625]=0.2993;z[625]=0.0001;
x[630]=0.7079;y[630]=0.2920;z[630]=0.0001;
x[635]=0.7140;y[635]=0.2859;z[635]=0.0001;
x[640]=0.7219;y[640]=0.2809;z[640]=0.0001;
x[645]=0.7230;y[645]=0.2770;z[645]=0.0000;
x[650]=0.7260;y[650]=0.2740;z[650]=0.0000;
x[655]=0.7283;y[655]=0.2717;z[655]=0.0000;
x[660]=0.7300;y[660]=0.2700;z[660]=0.0000;
x[665]=0.7311;y[665]=0.2689;z[665]=0.0000;
x[670]=0.7320;y[670]=0.2680;z[670]=0.0000;
x[675]=0.7327;y[675]=0.2673;z[675]=0.0000;
x[680]=0.7334;y[680]=0.2666;z[680]=0.0000;
x[685]=0.7340;y[685]=0.2660;z[685]=0.0000;
x[690]=0.7344;y[690]=0.2656;z[690]=0.0000;
x[695]=0.7346;y[695]=0.2654;z[695]=0.0000;
x[700]=0.7347;y[700]=0.2653;z[700]=0.0000;
x[705]=0.7347;y[705]=0.2653;z[705]=0.0000;
x[710]=0.7347;y[710]=0.2653;z[710]=0.0000;
x[715]=0.7347;y[715]=0.2653;z[715]=0.0000;
x[720]=0.7347;y[720]=0.2653;z[720]=0.0000;
x[725]=0.7347;y[725]=0.2653;z[725]=0.0000;
x[730]=0.7347;y[730]=0.2653;z[730]=0.0000;
x[735]=0.7347;y[735]=0.2653;z[735]=0.0000;
x[740]=0.7347;y[740]=0.2653;z[740]=0.0000;
x[745]=0.7347;y[745]=0.2653;z[745]=0.0000;
x[750]=0.7347;y[750]=0.2653;z[750]=0.0000;
x[755]=0.7347;y[755]=0.2653;z[755]=0.0000;
x[760]=0.7347;y[760]=0.2653;z[760]=0.0000;
x[765]=0.7347;y[765]=0.2653;z[765]=0.0000;
x[770]=0.7347;y[770]=0.2653;z[770]=0.0000;
x[775]=0.7347;y[775]=0.2653;z[775]=0.0000;
x[780]=0.7347;y[780]=0.2653;z[780]=0.0000;
xx=x[b];yy=y[b];zz=z[b];mi=32768;
for(int i=0;i<=255;i++)
for(int j=0;j<=255;j++)
for(int k=0;k<=255;k++)
{
if(i+k+j>0)
{
rr=0.490*i+0.310*j+0.200*k;
rr=rr/(0.667*i+1.132*j+1.200*k);
gg=0.117*i+0.812*j+0.010*k;
gg=gg/(0.667*i+1.132*j+1.200*k);
bb=0.000*i+0.010*j+0.990*k;
bb=bb/(0.667*i+1.132*j+1.200*k);
m=(rr-xx)*(rr-xx)+(gg-yy)*(gg-yy)+(bb-zz)*(bb-zz);
if(m<mi)
{
mi=m;
rrr=i;
ggg=j;
bbb=k;
}
}
}
printf("R:%d G:%d B:%d",rrr,ggg,bbb);
for(int i=1;i<=1024;i++)
for(int j=1;j<=1024;j++)
{
a[i][j][0]=rrr;
a[i][j][1]=ggg;
a[i][j][2]=bbb;
}
for(int j=0;j<DIM;j++)
for(int i=0;i<DIM;i++)
pixel_write(i,j);
fclose(fp);
system("pause");
return 0;
}
void pixel_write(int i, int j)
{
static unsigned char color[3];
for (int k=0;k<3;k++)
color[k] = a[i][j][k]&255;
fwrite(color, 1, 3, fp);
}程序在下面的链接也会附加给大家下载学习。picture_make.cpp
程序运用与检验
由于在这之前没有人做过波长与颜色转化的相关尝试,所以我们也算是这种算法的创始人了(自吹自擂)。令人振奋的是该程序在多次检验调试后终于到达了最优状态,下面我就展示该程序的效果。
经过双缝干涉测量,红光的波长为620nm左右,将其放入程序检验。
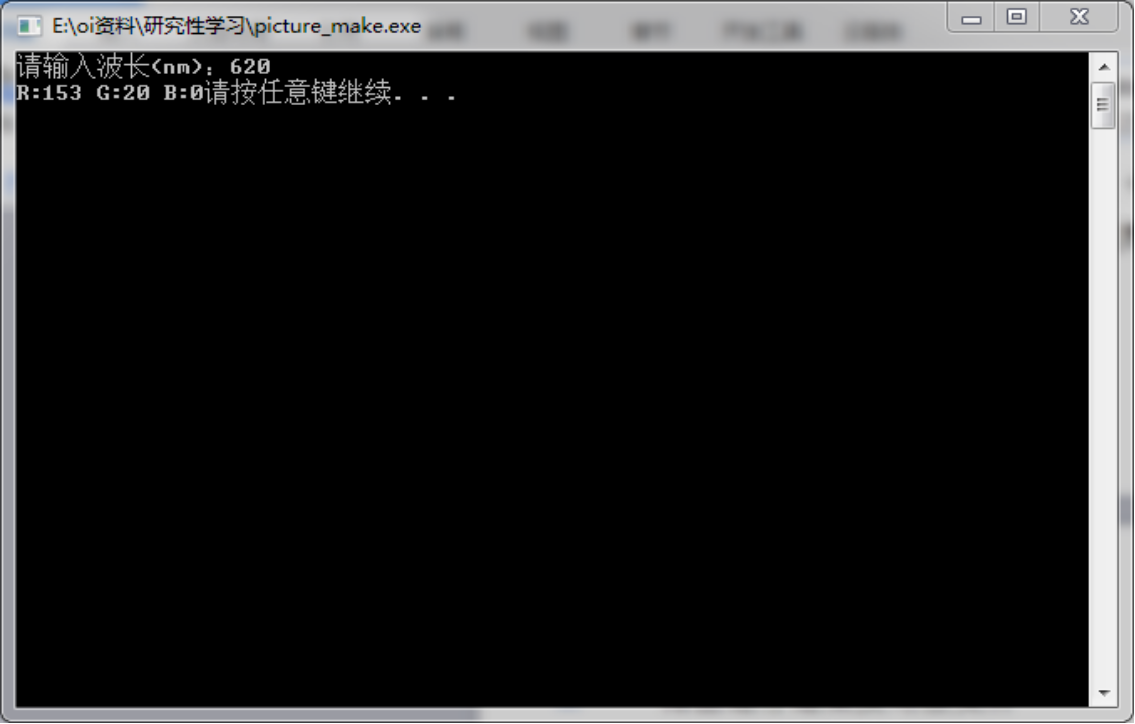
并打开对应的输出文件。
输出颜色为红色,颜色及RGB值符合观察所测值。
同理对绿光波长进行测试(观测得绿光波长约为510nm)

并打开对应的输出文件。
输出颜色为绿色,颜色及RGB值符合观察所测值。至此,程序的效果及正确性展示完成。
结语及展望
由上面的测试我们可以发现。该程序能快速有效的计算出波长与RGB颜色的对应关系,这将极大的便利艺术工作者及人类日后的生活,对艺术乃至人类视觉进步的发展有着极其深远的影响!
参考文献
最后的最后特别鸣谢以下参考文献!!!
《CIE1931色度图解析》-百度文库
《色度图波长对应坐标值》-百度文库

那請問要如何得到像洋紅色這樣非單一波長光的複合光色?( ´・ω・)ノ"(っω・ˋ。)
把所有波长对应的rgb都画出来,结果是红到蓝,没有紫色,所以其实算出来的是不对的,偏差有几十nm,红绿测试正确是因为偏差之后的颜色仍然是红/绿色。
最后还是用的以下的方法算的:
https://blog.csdn.net/m0_37816922/article/details/103457744
380-455是紫色,这个算法表现不出来
请问博主,这句话m=(rr-xx)(rr-xx)+(gg-yy)(gg-yy)+(bb-zz)*(bb-zz)是什么意思?
这句话是计算现在的解的误差哦,我们最后选取的答案就是误差或者说偏差最小的那个
博主,怎么联系你,请教问题?我研究了一个颜色传感器,测试会得到F1-F8这8个波段的值还有一个clear及NIR的值,如何把这些值通过计算转到LAB或是XYZ?
博主您好, 您在x[520]处的数值设置有点小错误,应该是x[520] = 0.0743.
感谢您对蒟蒻BLOG的厚爱!错误已经更正,感谢感谢!!
厉害哟 少年程序大佬
没有没有还有很多东西要学呢QwQ
博主您好!感谢您的代码帮助到了我!您可能有一个小地方敲错了:42行的z[400] --> z[440]
谢谢您的指正!错误已经更改,感谢您对蒟蒻的BLOG的厚爱!
请问一下RGB转波长该怎么实现呢,谢谢了
诶……这边给出一个可行解吧,就是先通过这个x=(0.490r+0.310g+0.200b)/(0.667r+1.132g+1.200b)
y=(0.117r+0.812g+0.010b)/(0.667r+1.132g+1.200b)
z=(0.000r+0.010g+0.990b)/(0.667r+1.132g+1.200b)
把色度坐标算出来,然后再带入表格寻找波长,或者通过其他计算途径把色度坐标转化为波长_(:з」∠)_最后谢谢你阅读这篇BLOG!
至于其他更加简便计算途径,应该是有的,但博主最近要高考了,没有时间去算了,很抱歉望见谅QwQ
你好,你这个由波长转换成x,y,z是如何做到的呢
是有公式进行计算的呢,详细请见参考文献中的《色度图波长对应坐标值》-百度文库,最后感谢你阅读这篇BLIOG,祝您生活愉快!
博主:您好!我能向您请教细节的问题吗?我现在要做的就是反向的过程,即从RGB到波长的转换!
现在做出来了吗,怎么做出来的呀
博主,您好!可以向您请教细节的问题吗?我现在面临的问题和您的这个是颠倒过来的,我需要从RGB转换成波长!
诶……没有研究过比较简便的方法,这里提供两种解决方案吧,首先RGB值最多才256246256才不足两千万个……实在不行用我的算法打个表就出来了(可能有点大);当然,你已经知道了RGB值,就可以直接计算出色度坐标,接着只要O(n)扫描一遍,寻找差值最小的波长就是要求解的啦!
您的色度坐标和波长之间有公式计算吗?
然后x,y,z值计算得出后参照我给出的那个表寻找对应的波长就行了!
x=(0.490r+0.310g+0.200b)/(0.667r+1.132g+1.200b)
y=(0.117r+0.812g+0.010b)/(0.667r+1.132g+1.200b)
z=(0.000r+0.010g+0.990b)/(0.667r+1.132g+1.200b)
这个就是呢,我就是根据这个枚举出RGB值的。
嗯,这个是x,y,z与R,G,B之间的转化,有没有波长bz和x,y,z之间的转换公式,您的博文上写的是经过数学计算的出来的表格!
没有直接推到过x,y,z到波长耶……只有波长到x,y,z,不过可以给出一种解决方案,就是在计算得出x,y,z值后,用程序直接判断与波长为多少的光的x,y,z值最接近直接来得出一个近似的答案……现在博主高三了可能没那么多时间继续推了,望谅解QwQ
好的,多谢博主,棒棒哒!祝高考顺利!
谢谢谢谢!最后感谢您喜欢这篇BLOG,祝您生活愉快!OωO
你怎么这么优秀
您比较优秀ORZ