在之前的BLOG中，我们已经一同学习了如何将正则化运用到线性回归中。这篇BLOG，就让我们看看如何将正则化运用到我们熟悉的逻辑回归当中吧。

逻辑回归

对于逻辑回归，我们在之前一同学习了两种解决方法。一种是通过梯度下降法进行求解，另一种是用 Octave 中的高级优化算法进行求解。这两种方法都需要我们自行编程计算出代价函数 J(θ) 及其关于 θ0 到 θn 的偏导数。

我们之前也见到过，对于逻辑回归，在次数太高或者参数太多的情况下，也会出现过度拟合的情况：

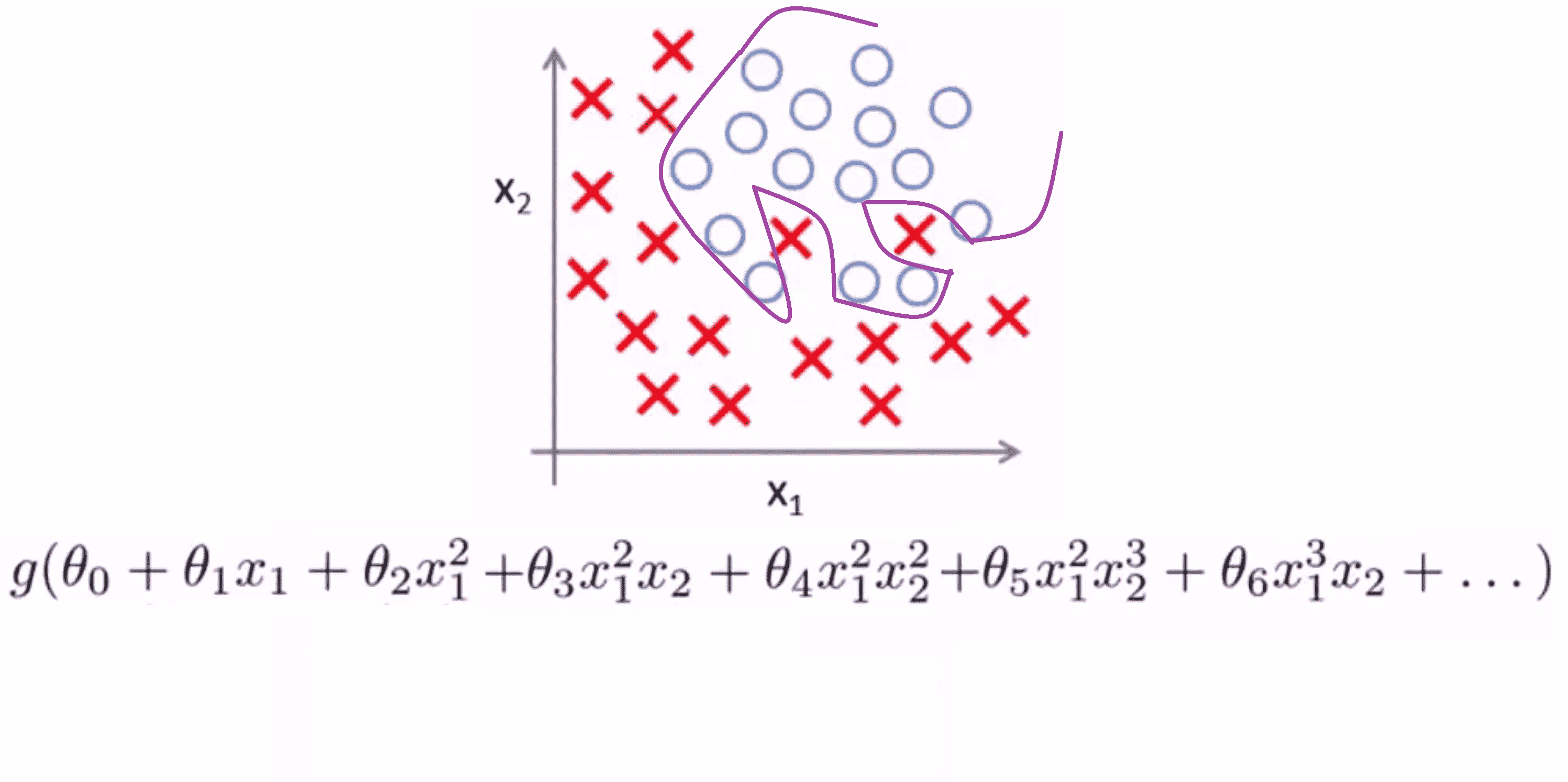
其中 g 是一个s型函数。下面就算我们没有正则化的逻辑回归代价函数：

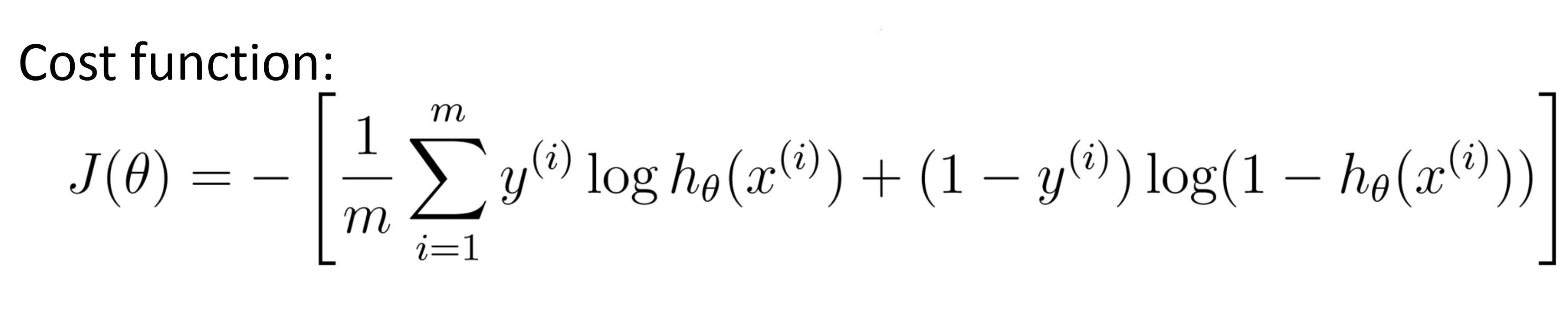
如果要进行正则化，我们就要对上面这个代价函数进行改写。我们所要做的就是在代价函数后加上对参数 θ1 到 θn 的惩罚，来防止它们过大：

这样做产生的结果就是，就算我们拟合的式子次数很高，参数很多，我们仍然能得到一条比较平滑，适用度比较高的划分边界。

梯度下降

那我们如何在梯度下降中实现对正则化后逻辑回归的求解呢？和线性回归类似，由于我们惩罚的只是 θ1 到 θn ，所以我们首先要将梯度下降的式子拆开：

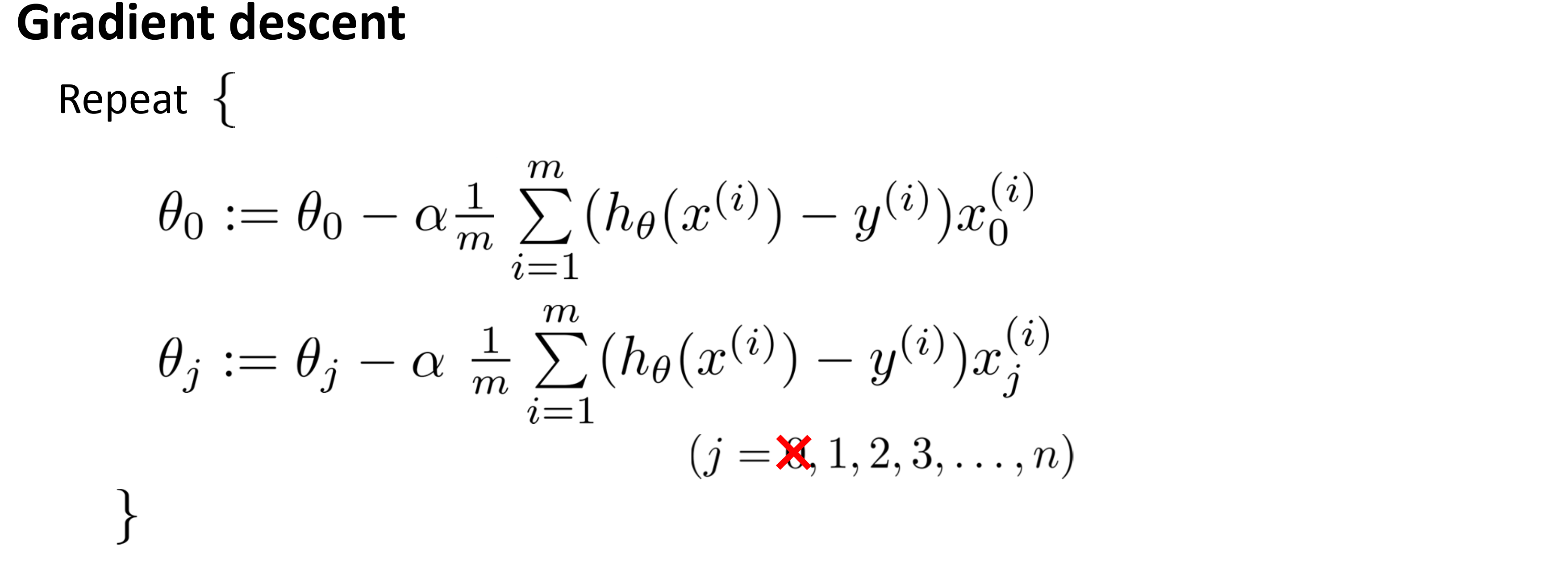
其中第一行是对 θ0 的更新，第二行是对 θ1 到 θn 的更新。接着我们将代价函数对 θ0 到 θn 求偏导数，就得到了下面这个过程：

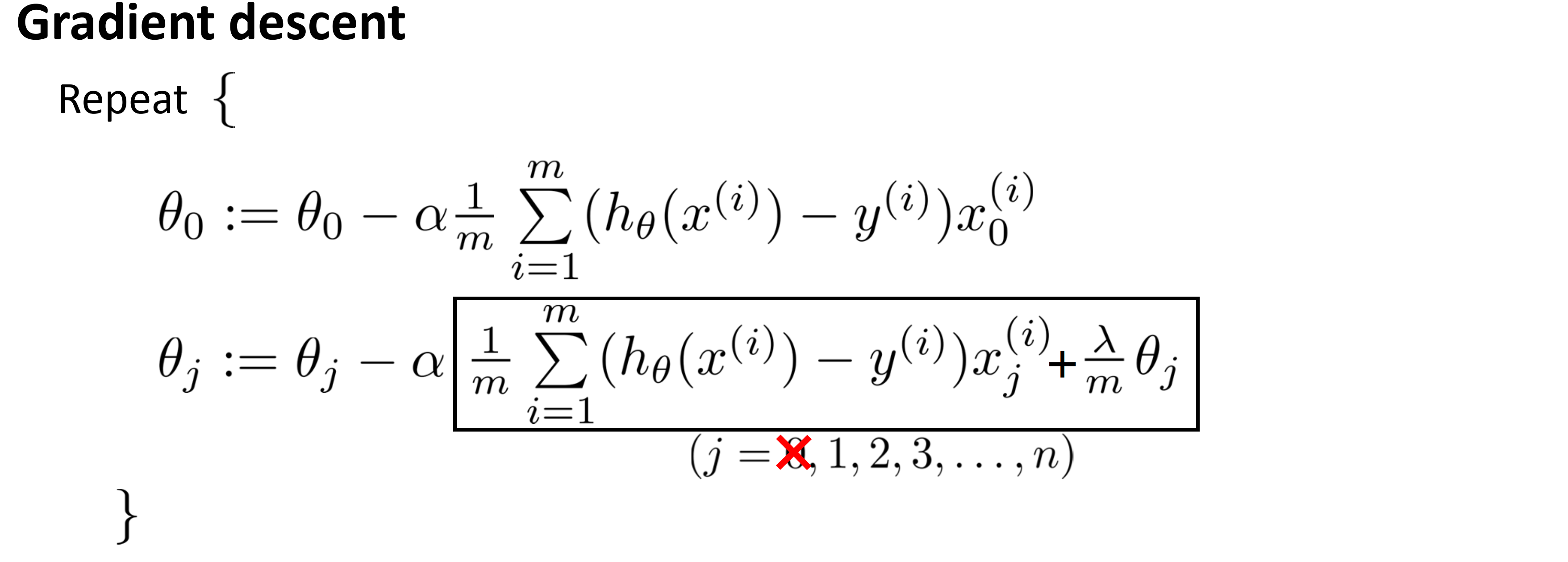
这个过程看起来和线性回归很像，但他们本质上是不同的，因为在这里，我们的假设函数 hθ(x) 是一个 S 型函数。

所以这就是用梯度下降求解正则化后的逻辑回归的过程。

算法实现

算法的思路在上面也说的很清楚了，下面展示cpp的代码实现，供大家参考学习：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
double lambd; 
double ans[11000];
double temp[11000], h[11000];
double x[11000][1100], y[11000];
const double Alpha = 3 * 1e-4;
const double e = 2.7182818284;
void read() {
    printf("请输入样本大小:\n");
    scanf("%d", &n);

    printf("请输入特征值的个数:\n");
    scanf("%d", &m);

    printf("请输入正则化参数:\n");
    scanf("%lf", &lambd);

    for(int i = 1; i <= n; i++) x[i][0] = 1;

    printf("请依次输入m个特征值xi和结果y(0 or 1):\n");
    for(int i = 1; i <=n; i++) { 
        for(int j = 1; j <= m; j++) {
            scanf("%lf", &x[i][j]);
        }
        scanf("%lf", &y[i]);
    }
    return;
}

void work() {
    memset(ans, 0, sizeof(ans));
    double delta = 1;
    int num;
    printf("请输入下降次数:\n"); 
    scanf("%d", &num);

    for(int o = 1; o <= num; o++) {
        for(int i = 0; i <= m; i++) temp[i] = (1 - Alpha * lambd / (double)n) * ans[i];
        //正则化！！！！ 
        //==========================================
        for(int i = 1; i <= n; i++) {
            h[i] = 0;
            for(int j = 0; j <= m; j++)
            {
                h[i] += x[i][j] * ans[j];
            }
            h[i] = 1 / (1 + pow(e, -h[i]));
            h[i] -= y[i];
        }
        //==========================================
        for(int i = 0; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                temp[i] = temp[i] - (Alpha / (double)m) * h[j] * x[j][i];
            }
        }
        //==========================================
        for(int i = 0; i <= m; i++) ans[i] = temp[i];
    }
    return ;
}

void write() {
    printf("决策边界为：");
    printf("y = %0.1lf", ans[0]);
    for(int i = 1; i <= m; i++) {
        if(ans[i] >= 0)printf(" + %0.1f * x%d", ans[i], i);
        else printf(" - %0.1f * x%d", -ans[i], i);
    }
    printf("\n");
}
int main() {

    read();
    work();
    write();
    return 0;
}  

优化算法

接下来我们来看看如何在更高级的优化算法中使用正则化。其实对于这些高级的算法，我们要做的就是写一个函数 costFunction 去计算 J(θ) 及其关于 θ0 到 θn 的偏导数，剩下的过程之前已经讲过了，不懂的同学可以点击这里。

我们聚焦于我们要编写的函数 costFunction ，这个函数以向量 θ 作为输入，记得 Octave 中最开始的下标是 1 ，所以 θ0 要写成 theta1；接着我们通过编写的函数去计算 J(θ) 及其关于 θ0 到 θn 的偏导数然后给到 fminunc 这个函数当中进行优化求解。下面就是我们 costFunction 的大致框架：

现在我们正在使用正则化，所以我们的代价函数和偏导数和之前的不太一样。我们可以仿照上面梯度下降求出的偏导数，得到下面这个框架：

和之前一样，由于 θ0 没有受到惩罚， J(θ) 关于 θ0 的偏导数项和没有正则化相比并没有发生变化，但对于其他的 θj ，都加上了一个项λ / m * θj。

而我们的 fminunc 在调用 costFunction 后，将会用优化的算法去最小化我们的 J(θ) ，且其返回的值就是正则化逻辑回归的解。

结语

通过这篇BLOG，相信你已经学会了如何求解正则化逻辑回归。到这里，你已经学会了线性回归，逻辑回归，梯度下降，高级优化算法和正则化，你对机器学习的理解已经超过很多人了。所以现在你已经有了足够的知识用机器学习去解决生活中的一些简单问题了。但我们仍然任重道远，要学的东西还有很多。最后希望你喜欢这篇BLOG！