在之前的BLOG里,我们一同学习了什么是正则化,这篇BLOG,就让我们把正则化运用在回归问题上吧。
线性回归
对于线性回归问题的求解,我们之前学习了两种学习算法,一种基于梯度下降,一种基于正规方程。现在就让我们分别看看如何将正规化运用到这两种方法上。
下图我们之前推导出的正则化线性回归的优化目标:
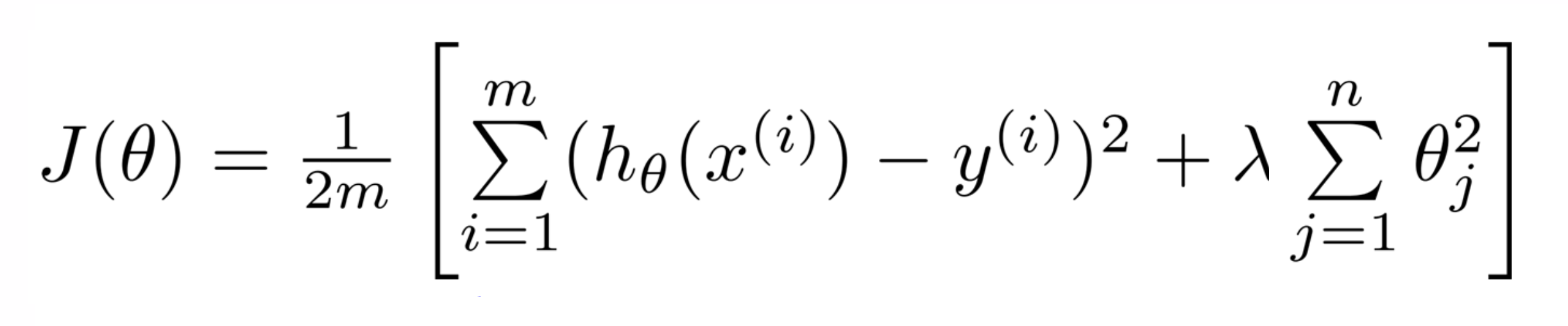
在中括号内的前面的第一部分是一般线性回归的目标代价函数,而后面那项则是额外的正则化项,其中 λ 是正则化参数。我们想找到参数 θ ,使得能最小化代价函数,即这个正则化代价函数 J(θ)。
下面就让我们看看两种算法分别要怎么操作。
梯度下降法
我们之前最常使用的就是用梯度下降求解原来没有正则项的代价函数。我们用下面的算法求解常规的没有正则项的线性回归:
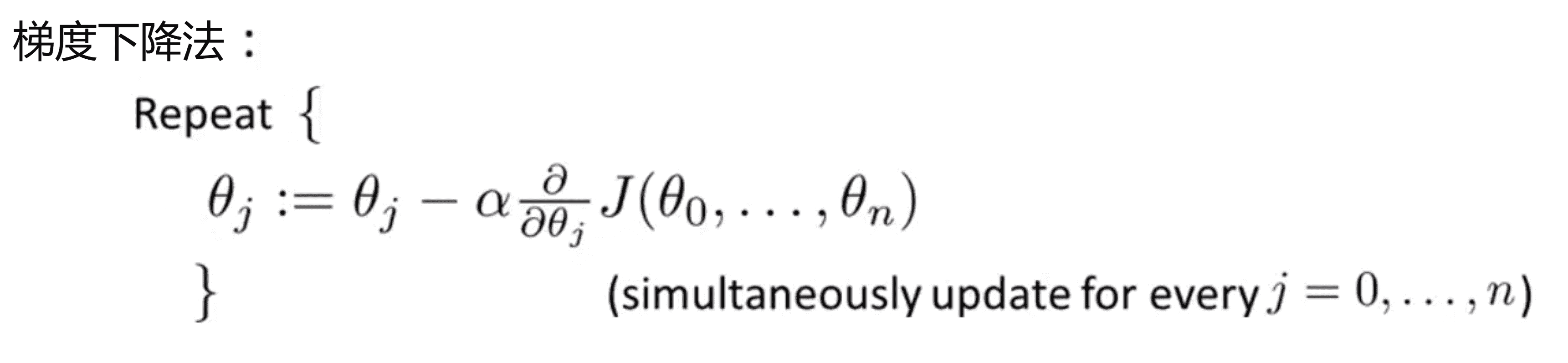
我们会反复进行如上操作来更新参数 θj,其中 j=0, 1, 2...n。但我们正则化的惩罚项只有 θ1 到 θn ,所以我们要先把 θ0 的更新分离出来,剩下的这些参数θ1, θ2 到θn的更新作为另一部分,而我们对于 θ1 到 θn ,其学习效率 α 后的项应该就是我们的代价函数对于 θj 的偏导数项,所以经过计算,我们得到的过程就如下:
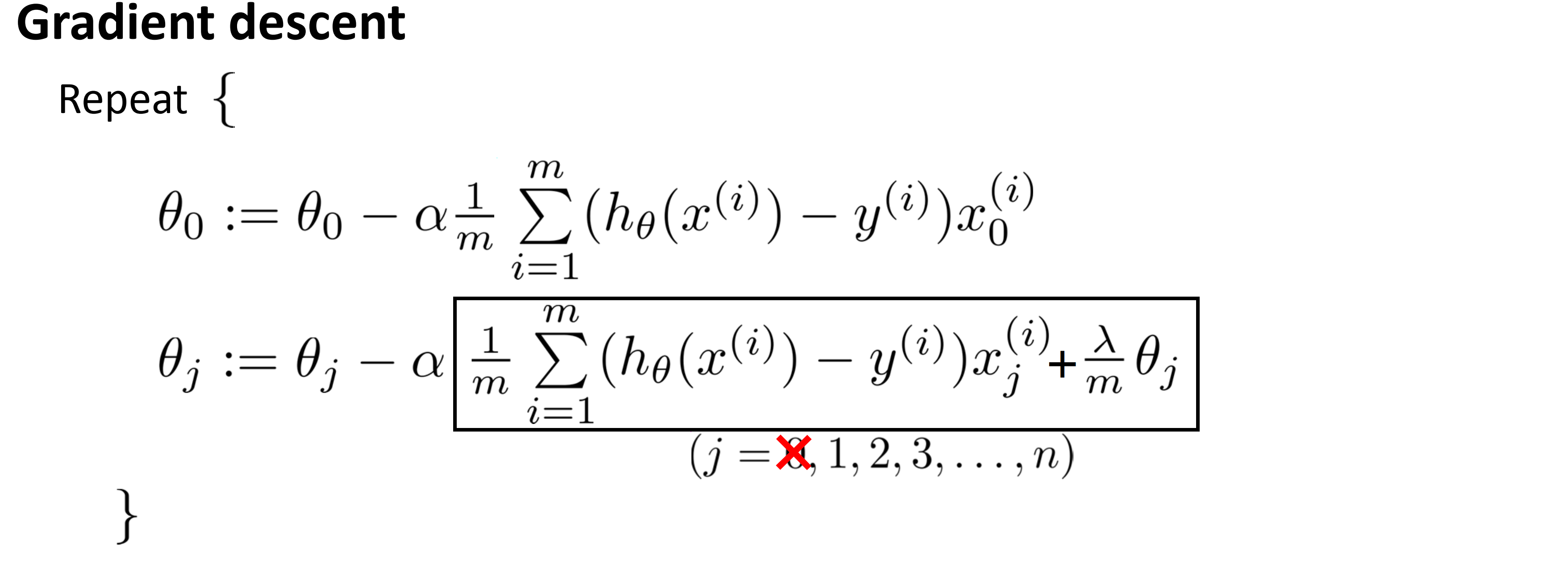
我们在原本偏导数的项后添加了一项:λ / m * θj ,这样我们就有了用于最小化正则化代价函数 J(θ) 的梯度下降算法。由于篇幅有限,我不打算用微积分来证明这一点,但不难证明,应该不难证明学习效率 α 后的项就是 J(θ) 对 θj 的偏导数。
我们将新添加的一项提出来:
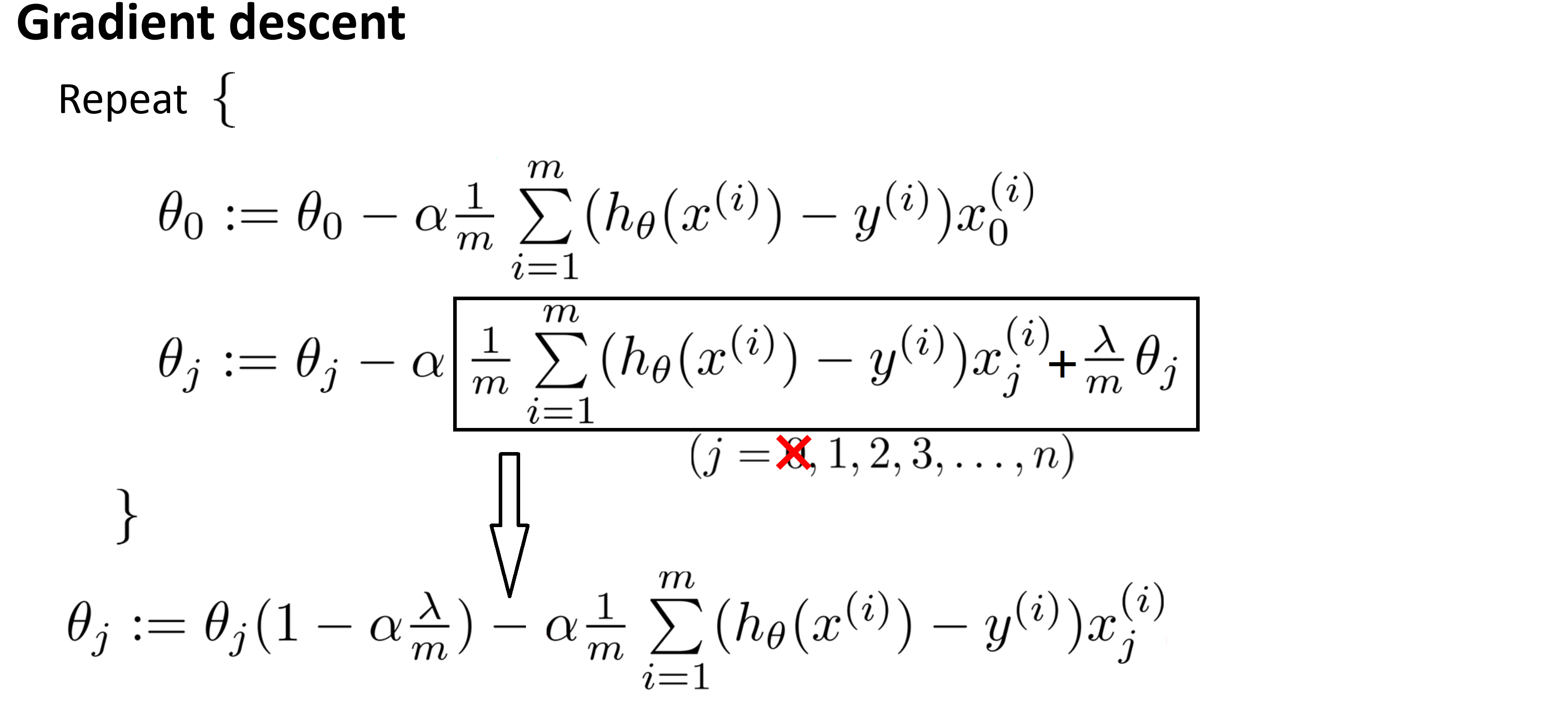
我们就会发现一些有趣的东西,具体来说 θj 的每次更新都是 θj *( 1 - α * λ / m) 后再前去没有正则化的偏导数项。而 ( 1 - α * λ / m) 通常是一个具体的实数而且小于 1 ,比如说是 0.99 吧;所以每次对 θj 更新的结果,可以看作是被替换为 θj 的 0.99 倍进行操作,这就把 θj 向 0 压缩了一点点,所以这使得 θj 的绝对值小了一点,更正式地说 θj^2 更小了。
所以总而言之当我们使用正则化线性回归时,我们需要做的就是在每一个被正规化的参数 θj 上乘以了一个比 1 小一点点的数字,这就把参数压缩了一点,然后我们执行跟以前一样的更新。当然这仅仅是我们从直观上认识,这个更新在做什么从数学上讲,其实就是对带有正则化项的 J(θ) 进行梯度下降算法。
代码实现
算法的思路都在上面了,同样地,这次我还是用cpp来是实现这个算法供大家交流学习:
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
double lambd;
double ans[11000];
double temp[11000], h[11000];
double x[11000][1100], y[11000];
const double Alpha = 3 * 1e-4;
void read() {
printf("请输入样本大小:\n");
scanf("%d", &n);
printf("请输入特征值的个数:\n");
scanf("%d", &m);
printf("请输入正则化参数:\n");
scanf("%lf", &lambd);
for(int i = 1; i <= n; i++) x[i][0] = 1;
printf("请依次输入m个特征值xi和结果y:\n");
for(int i = 1; i <=n; i++) {
for(int j = 1; j <= m; j++) {
scanf("%lf", &x[i][j]);
}
scanf("%lf", &y[i]);
}
return;
}
void work() {
memset(ans, 0, sizeof(ans));
double delta = 1;
int num;
printf("请输入下降次数:\n");
scanf("%d", &num);
for(int o = 1; o <= num; o++) {
for(int i = 0; i <= m; i++) temp[i] = (1 - Alpha * lambd / (double)n) * ans[i];
//正则化!!!!
//==========================================
for(int i = 1; i <= n; i++) {
h[i] = 0;
for(int j = 0; j <= m; j++)
{
h[i] += x[i][j] * ans[j];
}
h[i] -= y[i];
}
//==========================================
for(int i = 0; i <= m; i++) {
for(int j = 1; j <= n; j++) {
temp[i] = temp[i] - (Alpha / (double)m) * h[j] * x[j][i];
}
}
//==========================================
for(int i = 0; i <= m; i++) ans[i] = temp[i];
}
return ;
}
void write() {
printf("拟合出的直线为:");
printf("y = %0.1lf", ans[0]);
for(int i = 1; i <= m; i++) {
if(ans[i] >= 0)printf(" + %0.1f * x%d", ans[i], i);
else printf(" - %0.1f * x%d", -ans[i], i);
}
printf("\n");
}
int main() {
read();
work();
write();
return 0;
} 正规方程法
我们最小化 J(θ) 的第二种算法是使用正规方程,我们的做法是建立一个设计矩阵 X ,其中每一行对应于一个单独的训练样本,然后建立一个向量 y ,向量 y 是一个 m 维的向量 ,包含了所有训练集里的结果,所以 X 是一个 m × (n+1) 维的矩阵而 y 是一个 m 维向量:
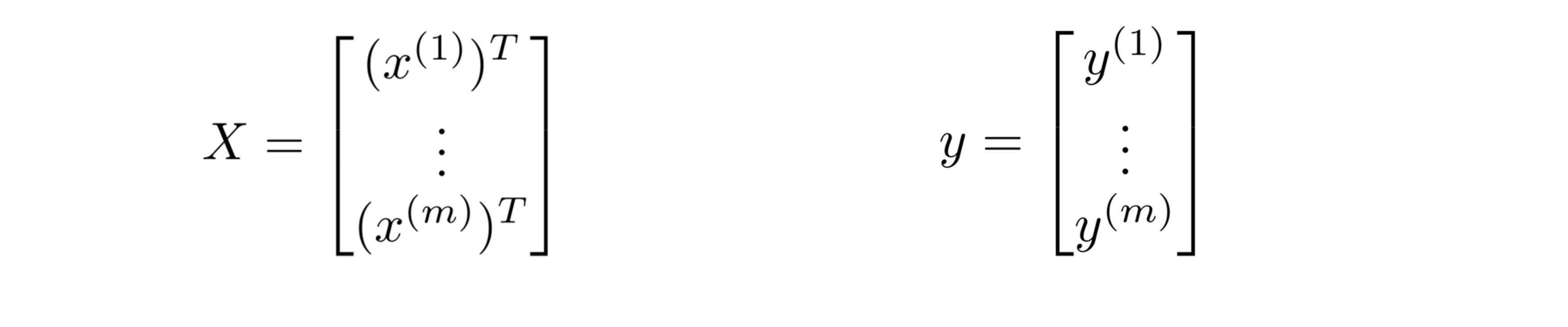
为了最小化代价函数 J(θ) 的一个办法就是让 θ 等于下面这个式子:
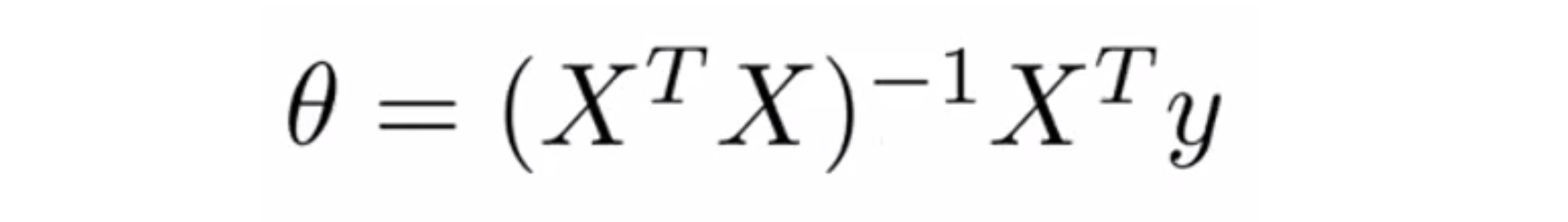
而计算得到的 θ 的值其实就是最小化代价函数 J(θ) 所对应的 θ 的值。这时的代价函数 J(θ) 没有正则项,现在如果我们用了是正则化,我们想要用正规方程得到最小值,我们应该怎么计算呢?推导的方法是取 J(θ) 关于各个参数的偏导数,并令它们等于 0 ,然后做些数学推导,我们就可以得到下面这样的一个式子,它使得代价函数最小:
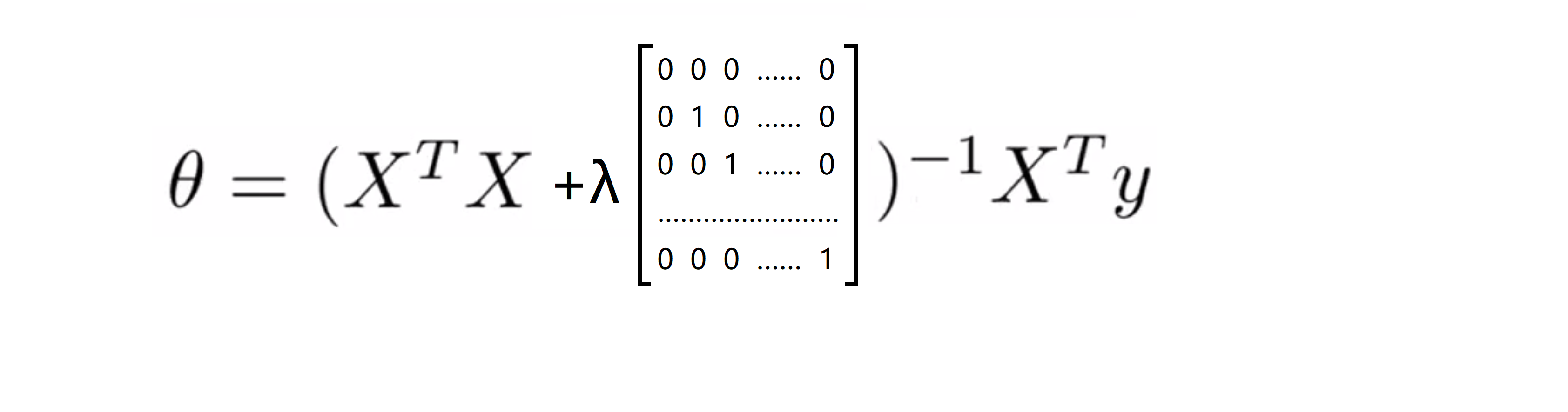
我们添加的矩阵左上角的元素是 0 ,其余对角线元素都是 1 剩下的元素也都是 0 ,且是一个 (n+1) × (n+1) 维的矩阵。同样地我不打算对这些作数学推导,但可以证明如果采用新定义的包含正则项的目标函数 J(θ) ,那么这个计算 θ 的式子能使你的 J(θ) 达到全局最小值。
最后我再谈一下不可逆性的问题,之前在许多情况下 X^T X 将是不可逆或奇异的(singluar) ,如果你在 Octave 里运行它,就算你用函数 pinv 取伪逆矩阵,但实际上还是不会得到一个很好的假设。但幸运的是正规化也为我们解决了这个问题,只要正则参数是严格大于0的,实际上可以证明 X^T X 加上 λ 乘以我们的补充矩阵在绝大多数情况下将是可逆的,这也为我们提供了极大的便利。
代码实现
算法的思路都在上面了,同样地,这次我还是用cpp来是实现这个算法供大家交流学习:
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
double lambd;
const double EPS = 1e-6;
double cpu[1100][2200];
double temp[1100][2200];
double x[1100][2200], y[1100];
double a[1100][2200],ans[2200];
const double Alpha = 3 * 1e-3;
void read() {
printf("请输入样本大小m:\n");
scanf("%d", &m);
printf("请输入特征值的个数n:\n");
scanf("%d", &n);
printf("请输入正则化参数:\n");
scanf("%lf", &lambd);
for(int i = 1; i <= m; i++) x[i][1] = 1;
n++;
printf("请依次输入m个特征值xi和结果y:\n");
for(int i = 1; i <= m ; i++) {
for(int j = 2; j <= n; j++) {
scanf("%lf", &x[i][j]);
}
scanf("%lf", &y[i]);
}
return;
}
void gauss() {
double multi;
for(int i = 1; i <= n; i++) {//从左到右枚举第i列(即枚举主元列)
if(fabs(a[i][i]) < EPS) {
printf("Error!\n");
exit(0);
}
multi = a[i][i];
for(int j = i; j <= 2 * n; j++) a[i][j] /= multi;
for(int j = 1; j <= n; j++) {
if(j != i) {
if(a[j][i] == 0)continue;
else multi= a[j][i] / a[i][i];
for(int k = i; k <= 2 * n; k++) {
a[j][k] -= a[i][k] * multi;
}
}
}
//通过初等行变化(即减去第i行的某个倍数),我们将除第i行的第i列都变成0;
}
}
void regularization() {
for(int i = 2; i <= n; i++) {
a[i][i] += lambd;
}
return ;
}//正则化!!!
void work() {
memset(ans, 0, sizeof(ans));
memset(cpu, 0, sizeof(cpu));
memset(a, 0, sizeof(a));
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
for(int k = 1; k <= m; k++) {
a[i][j] += x[k][i] * x[k][j];
}
}
}
regularization();//正则化!!!
for(int i = 1; i <= n; i++) {
a[i][i + n] = 1;
}
gauss();
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
temp[i][j] = a[i][j + n];
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
for(int k = 1; k <= n; k++) {
cpu[i][j] += temp[i][k] * x[j][k];
}
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
ans[i] += cpu[i][j] * y[j];
}
}
return ;
}
void write() {
printf("拟合出的直线为:");
printf("y = %0.1lf", ans[1]);
for(int i = 2; i <= n; i++) {
if(ans[i] >= 0)printf(" + %0.1f * x%d", ans[i], i);
else printf(" - %0.1f * x%d", -ans[i], i);
}
printf("\n");
}
int main() {
read();
work();
write();
return 0;
} 结语
通过这篇BLOG,相信你已经知道了如何实现正则化线性回归,利用它就可以避免过度拟,这应该可以让你在更多问题上更好地运用线性回归。在接下来的BLOG里,我们将把这种正则化的想法应用到逻辑回归。最后希望你喜欢这篇BLOG!