在之前的BLOG中，我们一同学习了如何用逻辑回归模型解决双类别的分类问题(即y = 0 或 1)，现在就让我们看看多类别的分类问题吧。

多类别分类问题

什么是多类别分类问题呢？我们先看这样一些例子，假如说我们现在需要一个学习算法能自动地将邮件归类到不同的文件夹里或者说可以自动地加上标签，比如来自工作的邮件、来自朋友的邮件 来自家人的邮件或者是有关兴趣爱好的邮件，那么我们就有了这样一个分类问题，其类别有四个分别用y = 1、y = 2、y = 3、 y = 4 来代表；另一个例子是有关药物诊断的，如果一个病人因为鼻塞来到你的诊所，他可能并没有生病，我们用 y = 1 这个类别来代表，或者患了感冒，我们用 y = 2 来代表，又或者得了流感 ，我们用 y = 3 来表示；最后一个例子，如果你正在做有关天气的机器学习分类问题，那么你可能想要区分哪些天是晴天、多云、雨天、 或者下雪天……

对上述所有的例子 y 可以取一个比较小的数值范围，比如 1 到 3 、 1 到 4 之类的，以上说的例子都属于多类分类问题。 顺便一提的是对于 y 的取值到底应该是 0 1 2 3 还是 1 2 3 4 其实都不重要，怎样标注都不会影响最后的结果。

然而对于之前的一个二元分类问题我们的数据看起来可能是像下图这样：

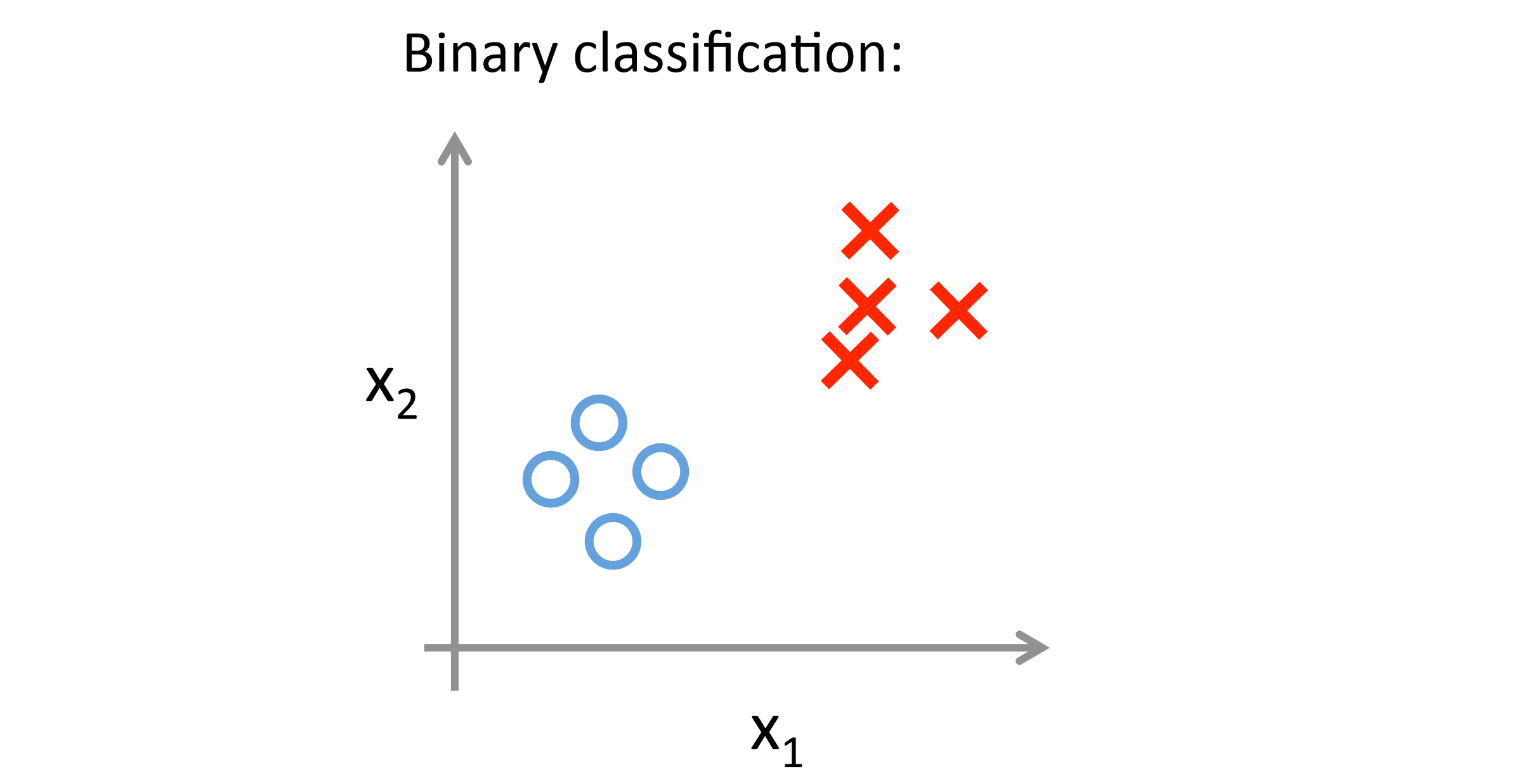
而对于一个多类分类问题我们的数据集或许看起来像下图这样，我们用三种不同的符号来代表三个类别：

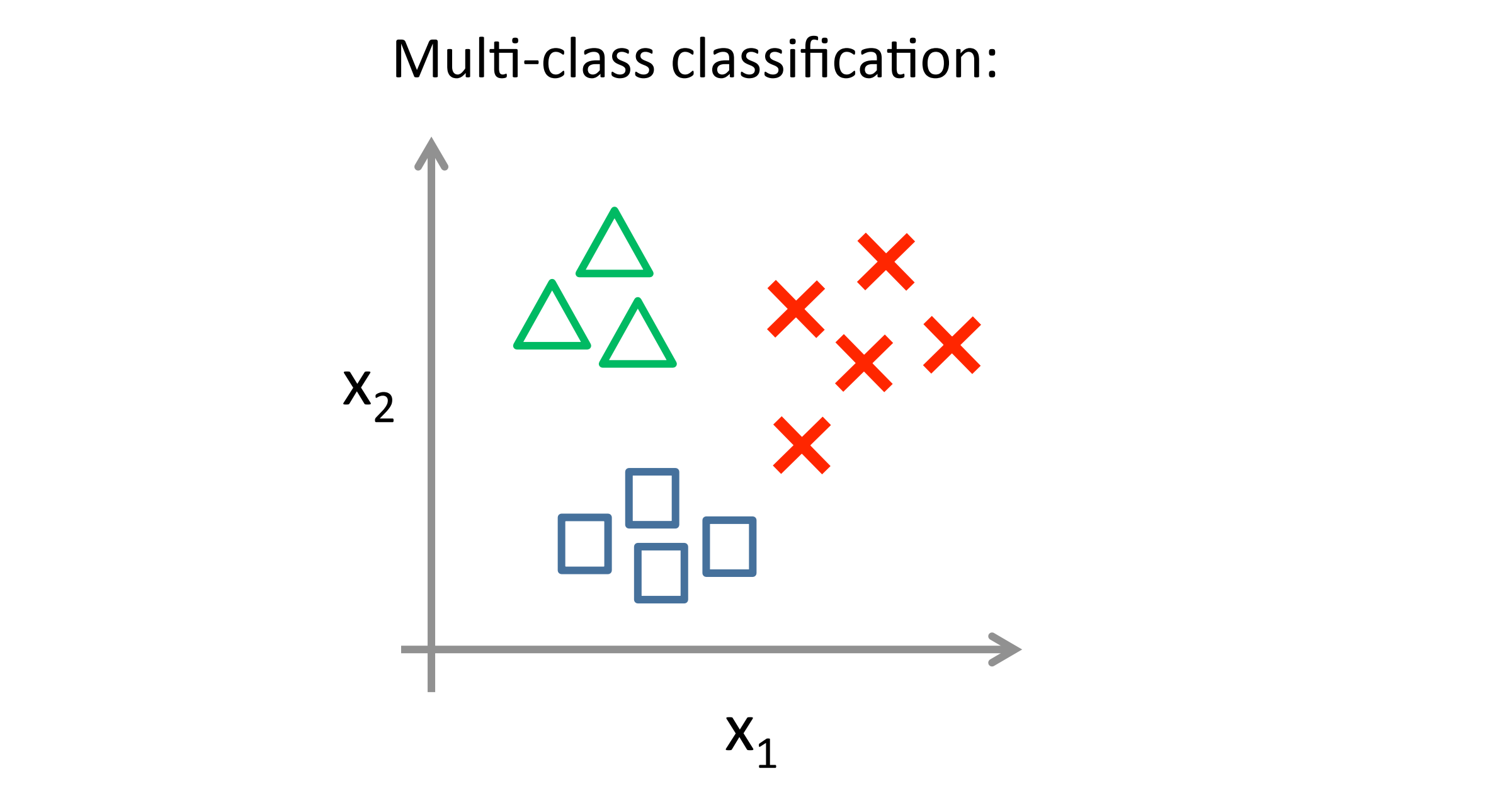
这就是多类别分类问题的大致情况。

一对多算法

那我们如何得到一个学习算法来进行分类呢？我们现在已经知道如何进行二元分类，我们可以使用逻辑回归模型进行求解，我们可以得到一条直线将数据集一分为二，分为正类和负类。

对于多类别分类问题，接下来我要介绍的，是被称为一对多(one-vs-all) 的算法。运一对多的分类思想，我们可以 将多类分类问题转化为二元分类问题。那具体要怎么操作呢？

让我们来看个例子。现在我们有一个训练集，好比下图表示我们有三个类别，我们用三角形表示 y = 1，矩形表示 y = 2，叉叉表示 y = 3：

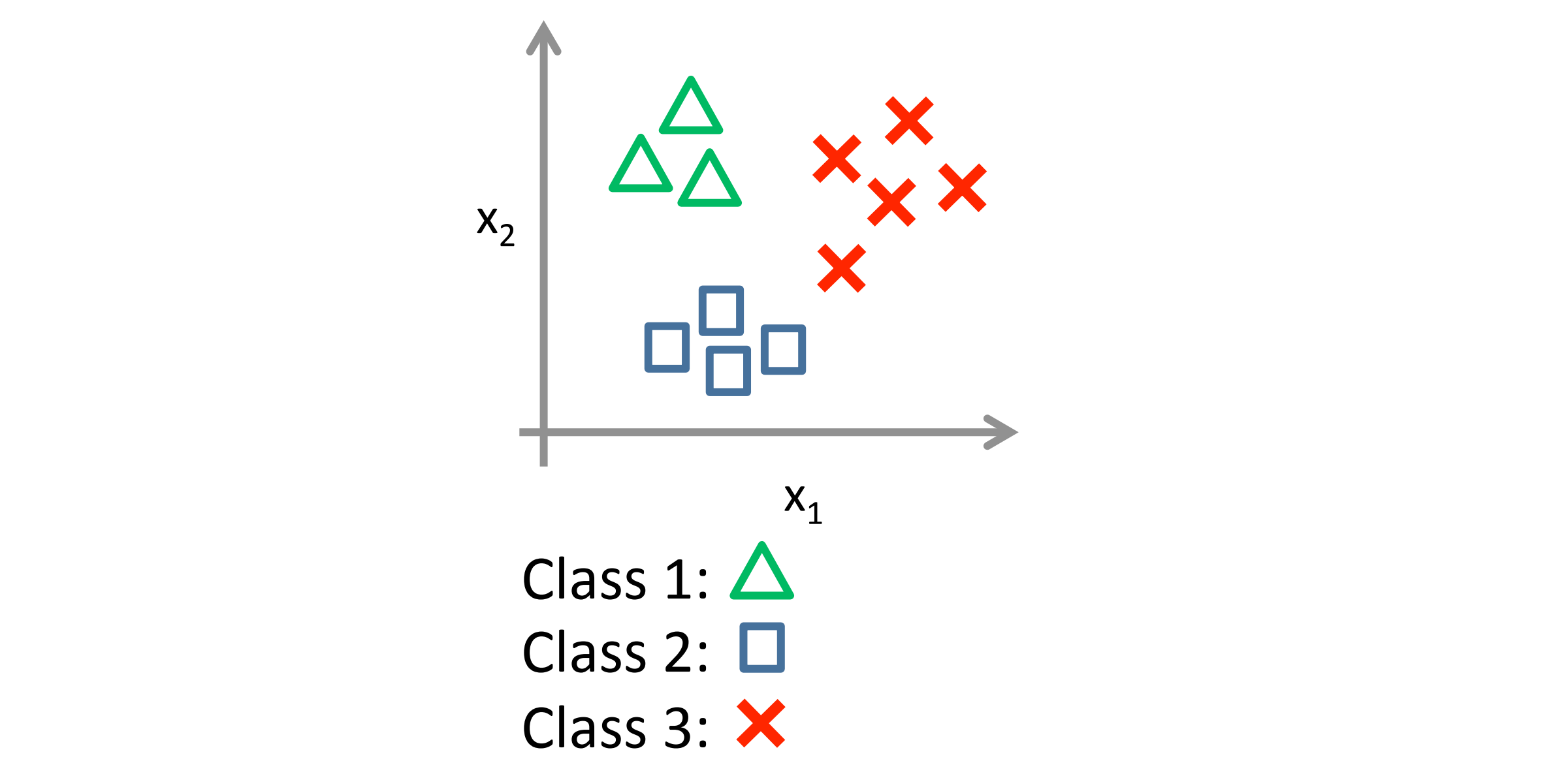
我们下面要做的就是运用一对多的思想，将其分成三个二元分类问题。我们先从用三角形代表的类别 1 开始，实际上我们可以创建一个新的"伪"训练集，我们定义类型 2 和类型 3 为负类，而类型 1 设定为正类，就如下图所示：

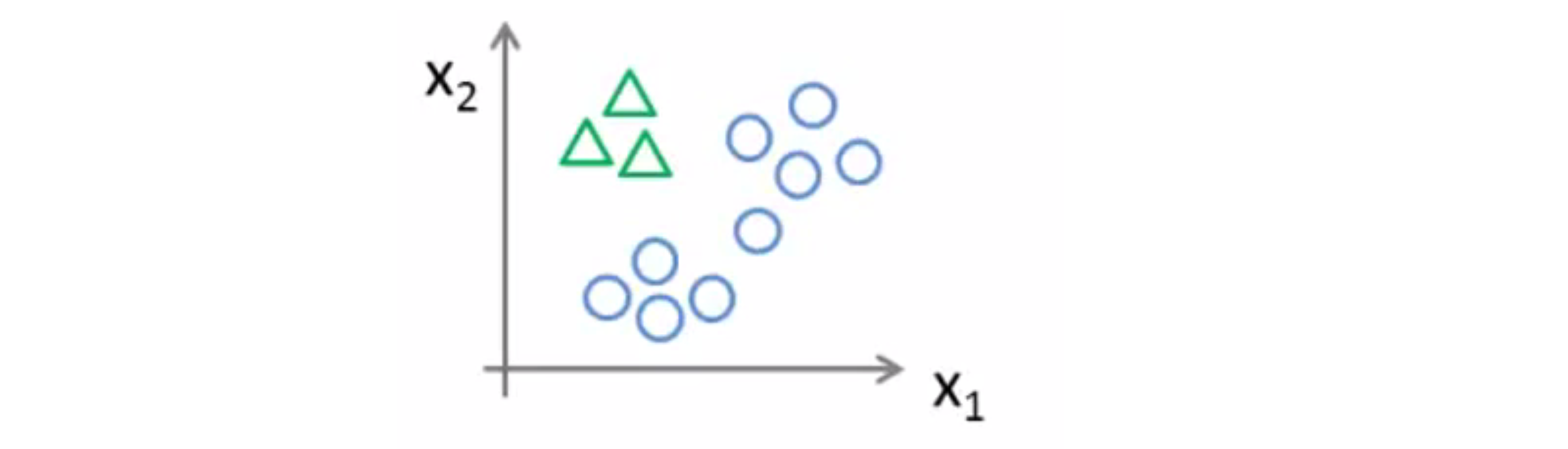
接着我们要拟合出一个合适的分类器，我们称其为(hθ^(1))(x)。在这路三角形是正样本，而圆形代表负样本。我们可以设置三角形的值为 1，圆形的值为 0，接着用梯度下降训练一个标准的逻辑回归分类器，这样我们就得到一个正边界：

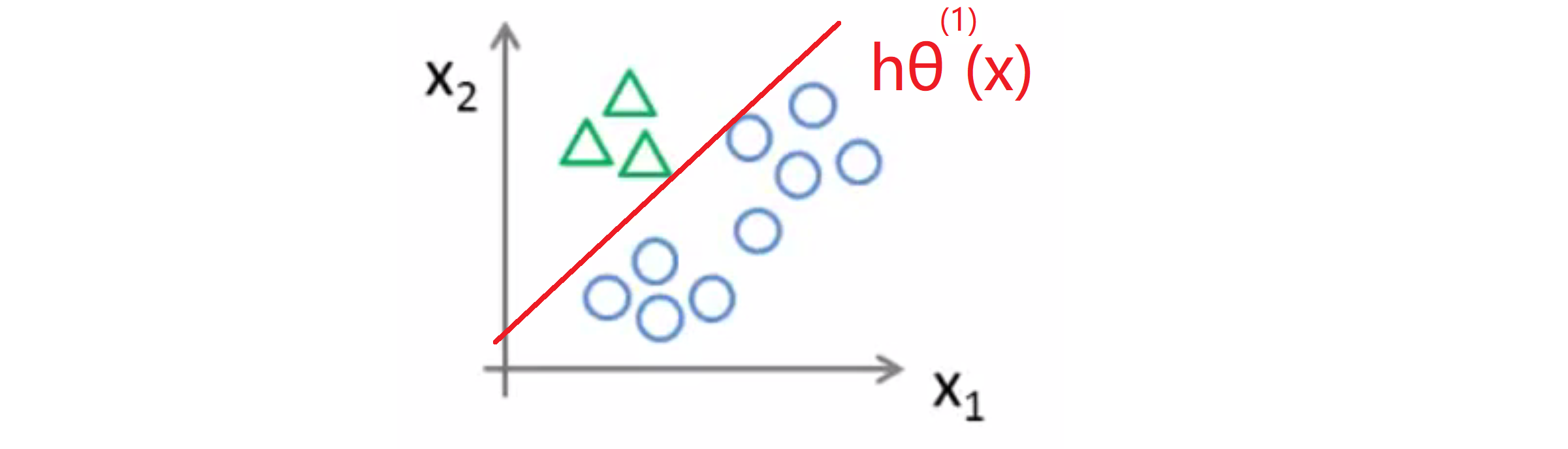
这里 hθ 的上标(1)表示类别 1 ,我们可以像这样对三角形类别一样为类别 2 做同样的工作：

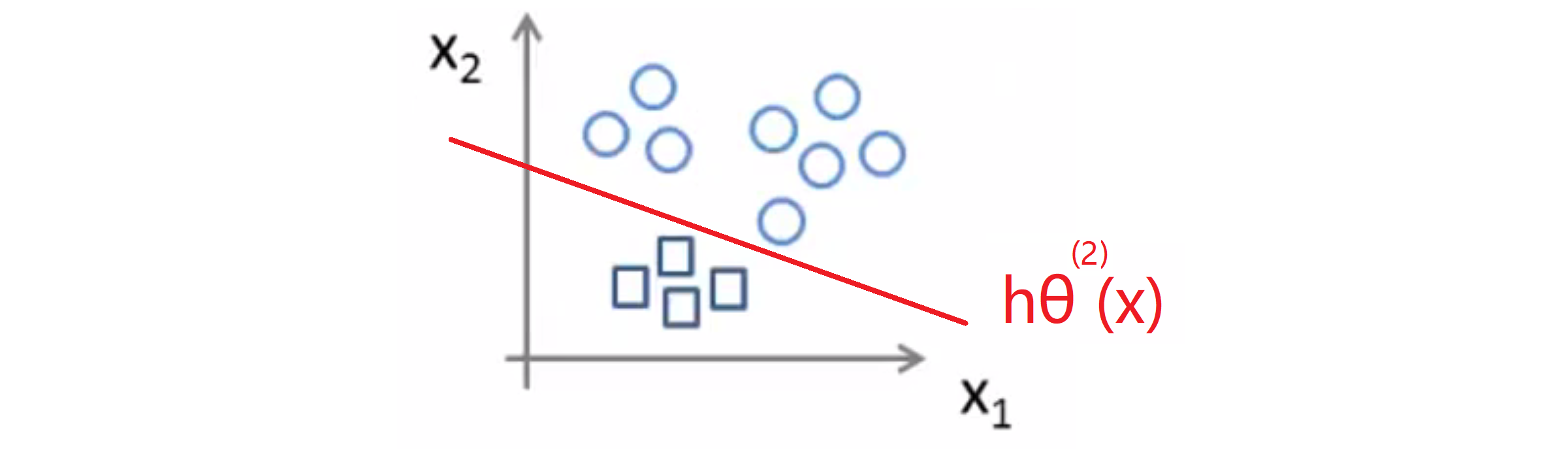
这样我们找到第二个合适的逻辑回归分类器，我们称为(hθ^(2))(x)，其中上标(2)表示 类别2，所以我们做的就是把方块类当做正样本，其他当成负样本进行分类。

最后同样地我们对类别 3 采用同样的方法，并找出第三个分类器 (hθ^(3))(x) ：

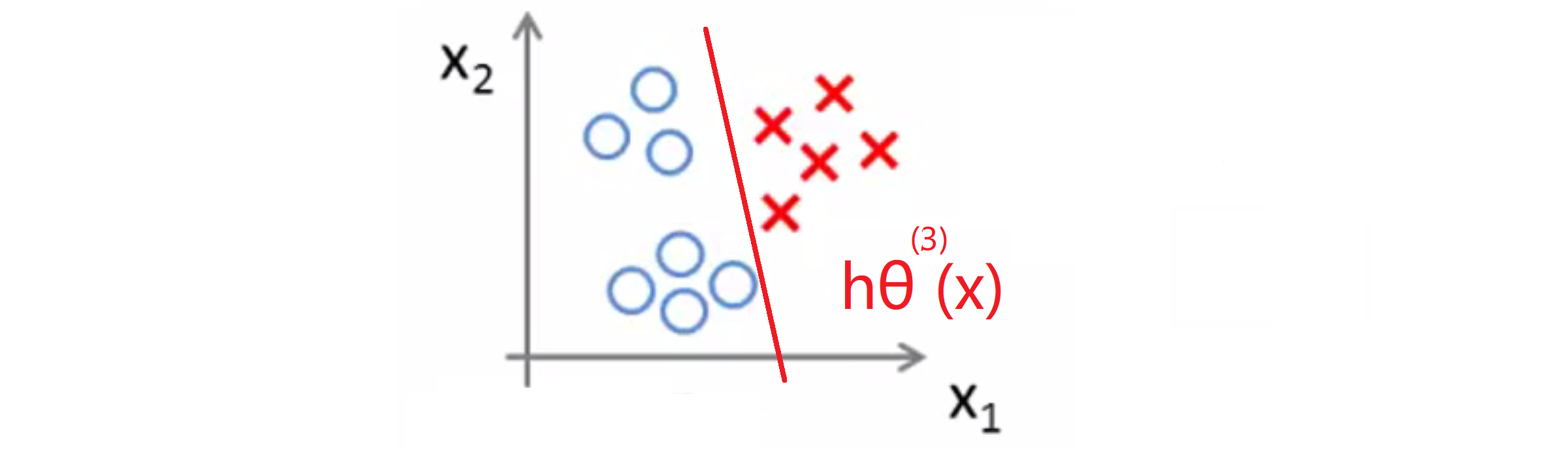
总而言之，我们对于 i 等于1、2、3都已经拟合出了分类器 (hθ^(i))(x)，那接下来我们可以怎么做呢？

对于一个新的数据，比如我们给出输入一个新的 x 值，怎么用这三个分类器进行预测呢？我们要做的就是在我们三个分类器里面分别输入 x ，然后我们选择一个让 h 最大的上标 i ，代表 x 最可能是第 i 个分类器中的正类也就是类型 i，可信度最高效果最好的就可认为得到一个正确的分类，无论i值是多少我们都有最高的概率去预测 y 就是那个值 。这样就可以解决多类别分类问题了。这就是多类别分类问题，以及一对多的算法，通过这个小算法，我们现在也可以将逻辑回归分类器用在多类分类的问题上了。

代码实现

算法原理在上面已经写的很清楚了，下面给出求出各分类器的cpp代码供大家交流学习，求出分类器后求解分类也非常简单就不再展示了：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m, k;
int num;
double ans[11000];
double temp[11000], h[11000];
double x[11000][1100], y[11000], z[11000];
const double Alpha = 3 * 1e-4;
const double e = 2.7182818284;
void read() {
    printf("请输入样本大小:\n");
    scanf("%d", &n);

    printf("请输入特征值的个数:\n");
    scanf("%d", &m);

    printf("请输入类型的个数:\n");
    scanf("%d", &k);

    for(int i = 1; i <= n; i++) x[i][0] = 1;

    printf("请依次输入m个特征值xi和结果y（1~k):\n");
    for(int i = 1; i <=n; i++) { 
        for(int j = 1; j <= m; j++) {
            scanf("%lf", &x[i][j]);
        }
        scanf("%lf", &z[i]);
    }
    return;
}

void work() {
    memset(ans, 0, sizeof(ans));
    memset(h, 0, sizeof(h));
    double delta = 1;

    for(int o = 1; o <= num; o++) {
        for(int i = 0; i <= m; i++) temp[i] = ans[i];
        //==========================================
        for(int i = 1; i <= n; i++) {
            h[i] = 0;
            for(int j = 0; j <= m; j++)
            {
                h[i] += x[i][j] * ans[j];
            }
            h[i] = 1 / (1 + pow(e, -h[i]));
            h[i] -= y[i];
        }
        //==========================================
        for(int i = 0; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                temp[i] = temp[i] - (Alpha / (double)m) * h[j] * x[j][i];
            }
        }
        //==========================================
        for(int i = 0; i <= m; i++) ans[i] = temp[i];
    }
    return ;
}

void write() {
    printf("决策边界为：");
    printf("y = %0.1lf", ans[0]);
    for(int i = 1; i <= m; i++) {
        if(ans[i] >= 0)printf(" + %0.1f * x%d", ans[i], i);
        else printf(" - %0.1f * x%d", -ans[i], i);
    }
    printf("\n");
}

void job() {
    printf("请输入下降次数:\n"); 
    scanf("%d", &num);
    for(int i = 1; i <= k; i++) {
        for(int j = 1; j <= n; j++) {
            if(int(z[j]) == i) y[j] = 1;
            else y[j] = 0;
        }
        work();
        printf("第 %d 个分类器的", i);
        write();
    }

}
int main() {

    read();
    job();
    return 0;
}  

可以看到效果还是不错的：

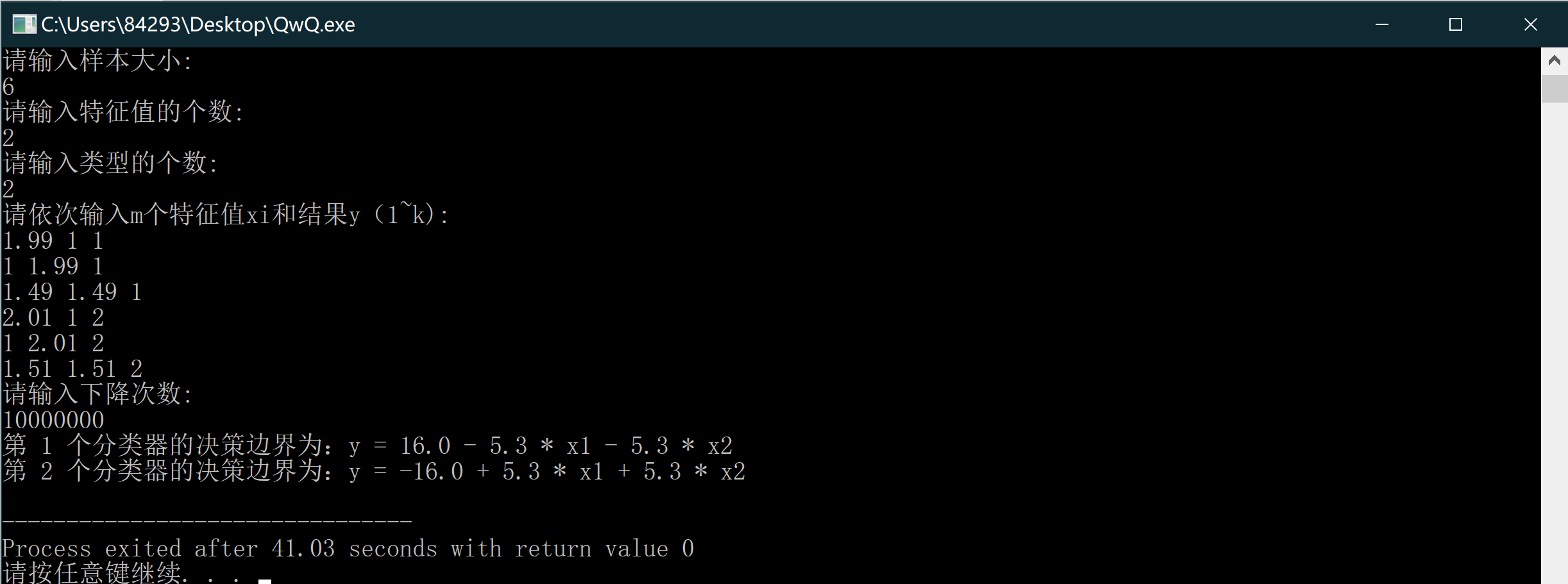
结语

通过这篇BLOG，相信你已经初步掌握了多类别分类问题的解法。到这里，分类问题就告一段落了。最后希望你喜欢这篇BLOG！