在之前的BLOG中，我们探讨了分类问题的逻辑回归模型。这篇BLOG，我们就将探讨逻辑回归的代价函数以及如何使用梯度下降法计算逻辑回归模型。

代价函数

让我们回顾一下我们的逻辑回归模型：

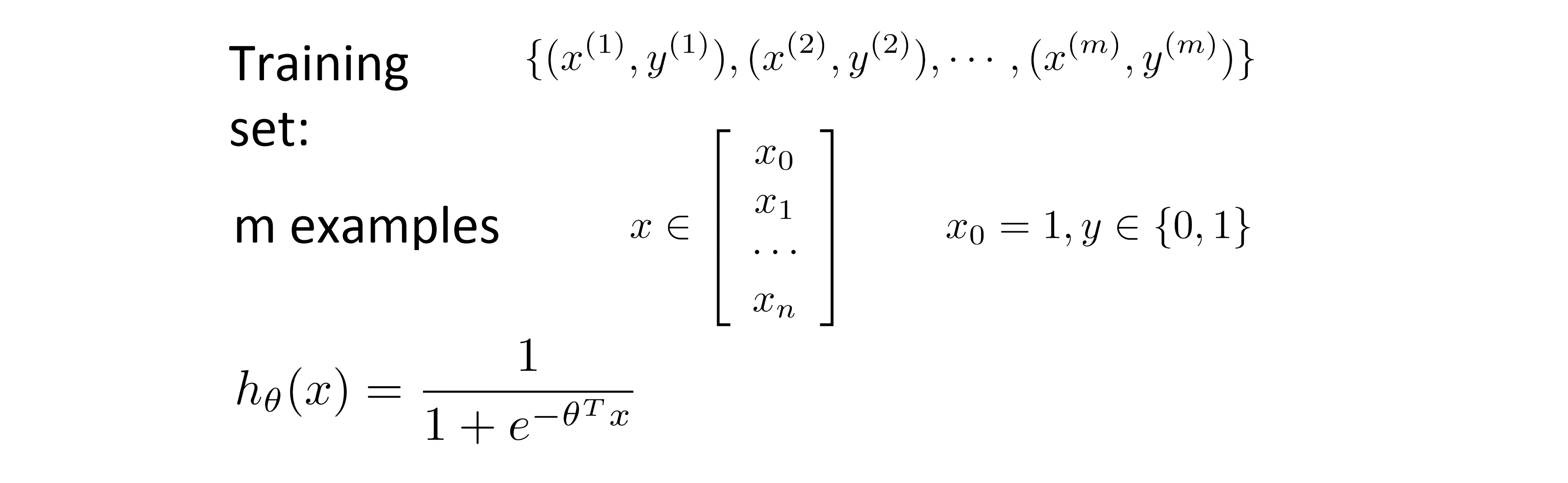
和线性回归模型一样，我们有一套训练集，我们的每个特征向量也和往常一样是 n + 1 维的（n是特征值的个数），其中 x0 恒等于1。而因为这是一个分类问题，所以我们的训练集的 y 都是 0 或 1 。hθ(x) 是我们的假设函数，现在我们的问题就是如何拟合参数θ？

在我们学习在线性回归模型中，我们使用了下面这样的代价函数。和之前稍微有些不同，我把一个 1/2 提到了 ∑ 后面：

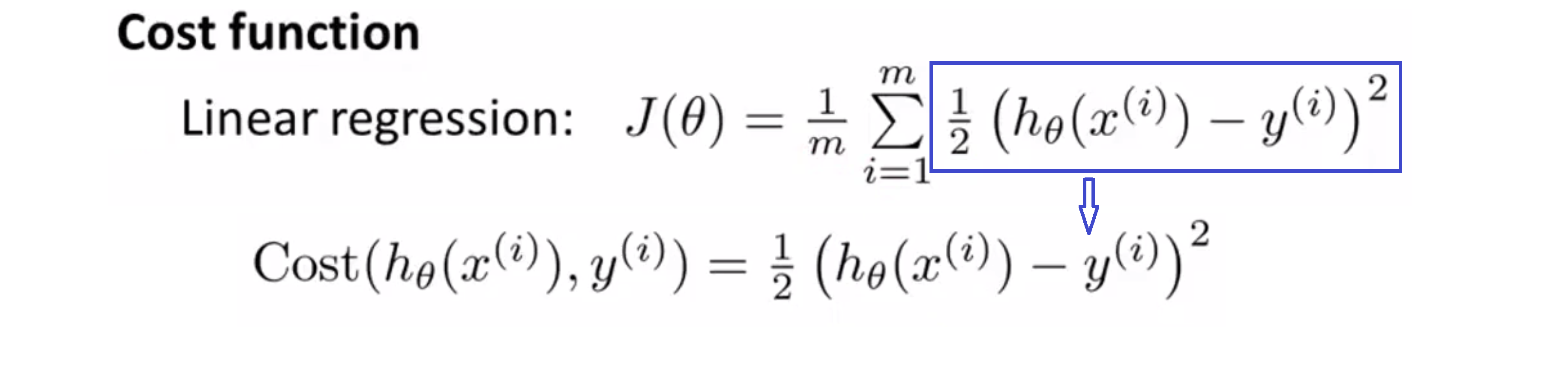
我们定义蓝框里的那部分就是第 i 个样本产生的代价，其就等于一半的平方误差。所以现在我们可以更清楚地看到代价函数是我的训练集每个样本产生代价的平均数。

以上的代价函数在线性回归中是很好用的，但在这里，我们要探讨的是逻辑回归的代价函数。那我们能否直接使用这个代价函数作为我们逻辑回归模型的代价函数呢？

如果我们把逻辑回归套进上面的代价函数，且我们可以求得代价函数的全局最小值，那么它就是可行的。但事实证明如果我们的逻辑回归使用用这个代价函数，那么得到的 Jθ 关于 θ 就是非凸的。什么是“凸”呢，下图中，左边就是非凸的，这意味着它有不止一个局部最小值，右边是凸的，这意味着它的局部最小值就是全局最小值：

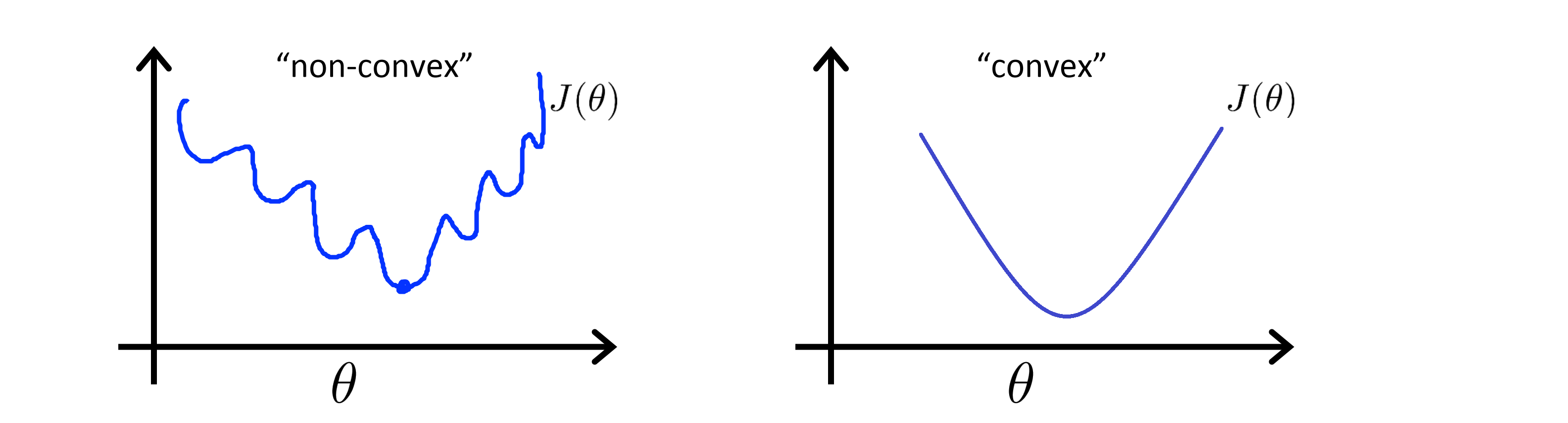
所以如果我们在一个非凸函数上跑梯度下降算法的话，就不能保证收敛到全局最小值。所以我们想做的是，想出一个新的代价函数，让逻辑回归模型应用上去得到的是一个凸函数，这样我们的梯度下降算法就能保证收敛到全局的最小值。

下面就是我们应用在逻辑回归上的代价函数：

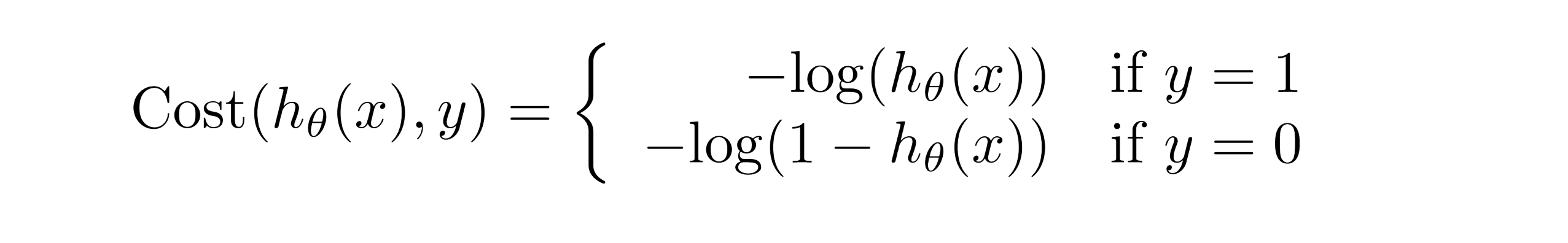
这看起来是个很复杂的函数，但让我们画出函数图像来直观感受一下这个代价函数先吧。

当y = 1时，代价函数如下图所示：

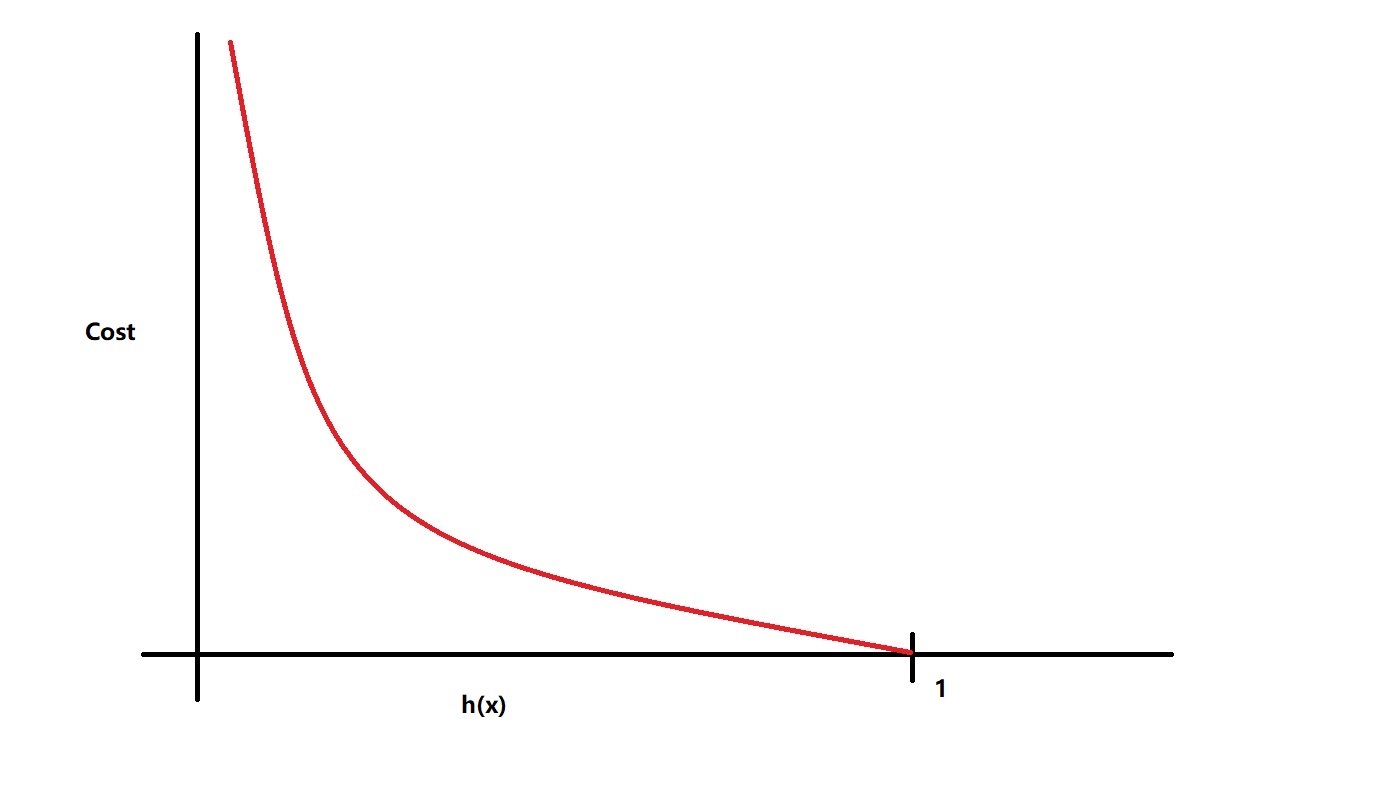
我们可以看到，此时当我们的预测值趋于 0 的时候(代表此时不可能有y = 1，预测得不准)，我们的代价就趋于正无穷；而当我们的预测趋于 1 (代表此时几乎可以肯定有y = 1，预测得准确)的时候，我们的代价就趋向于 0。

当y = 0时，代价函数如下图所示：

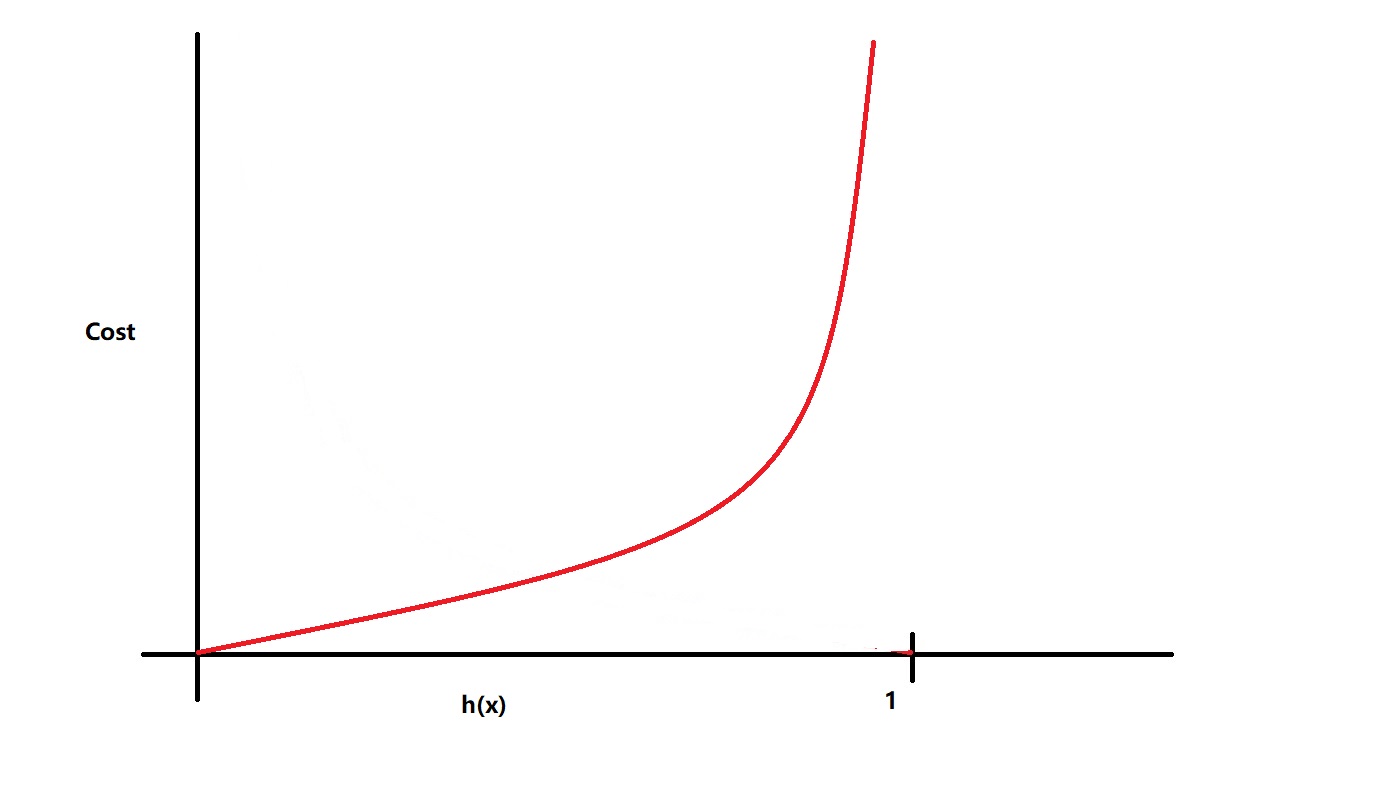
我们可以看到，此时当我们的预测值趋于 1 的时候(代表此时不可能有y = 0，预测得不准)，我们的代价就趋于正无穷；而当我们的预测趋于 0 (代表此时几乎可以肯定有y = 0，预测得准确)的时候，我们的代价就趋向于 0。

其实可以证明，我们选用的代价函数是凸函数，也就是其局部最优值就是全局最优值。接下来让我们看看如何化简这个代价函数。

代价函数的化简

现在我们来看看如何将我们的两段函数合写起来。下面是我们逻辑回归模型的代价函数：

注意，在这类分类问题中，我们 y 的取值只能是 0 或者 1，利用这个性质，我们可以把我们的代价函数合写起来：

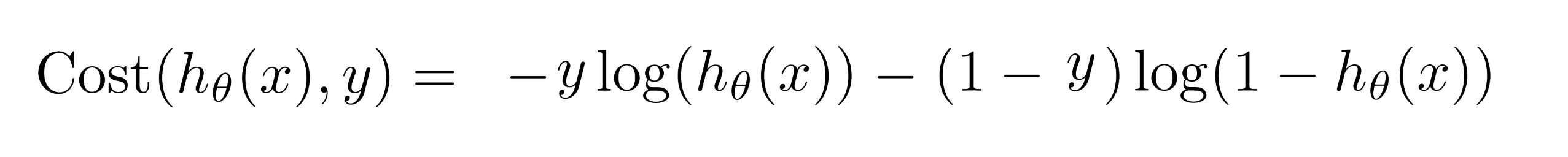
让我们看看为什么可以写成这样：我们知道 y 的取值只有两种可能—— 0 或者 1，让我们分别来看看。

当y = 1时，式子的右边-(1 - y)log(1 - hθ(x))就为 0 ，此时cost(hθ(x), y) = -ylog(hθ(x))，又因为此时y = 1，故有cost(hθ(x), y) = -log(hθ(x))；

当y = 0时，式子的左边-ylog(hθ(x))就为 0 ，此时cost(hθ(x), y) = -(1 - y)log(1 - hθ(x))，又因为此时y = 0，故有cost(hθ(x), y) = -log(1 - hθ(x))；这样代价函数就能简化成只用一行来表示。

这样我们就能写出我们总的代价函数：

那我们的代价函数为什么要写成这样呢？我们应该还有很多种选择？虽然我们这里没有严格的数学证明，但我可以告诉你，这个式子是通过统计学极大似然法的计算出来的，可以反应数据特征，且为凸函数，所以我们的逻辑回归的代价函数就选中了它。

梯度下降

我们在上一部分已经得到了我们逻辑回归模型的代价函数，且其关于 θ 是凸函数，所以我们就可以运用我们熟悉的梯度算法来通过最小化我们的代价函数 J(θ) 以得出我们关于数据集的参数 θ ，并以此来预测数据。

让我们来看看梯度下降法：

我们已经有了代价函数，剩下的就是要求解这个代价函数对每个变量的偏导数，即∂/∂j（J(θ)）。

如果你熟悉微积分的运算，你可以自己进行运算，但我可以告诉你，其实结果就如下：

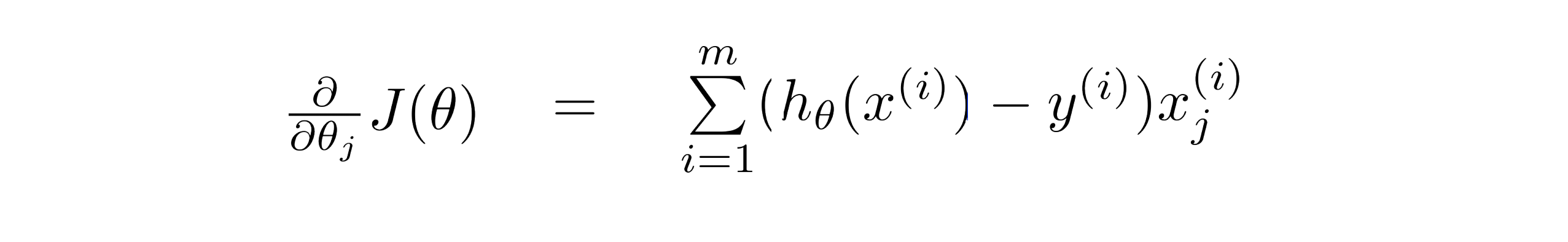
所以我们的梯度下降的过程就是：

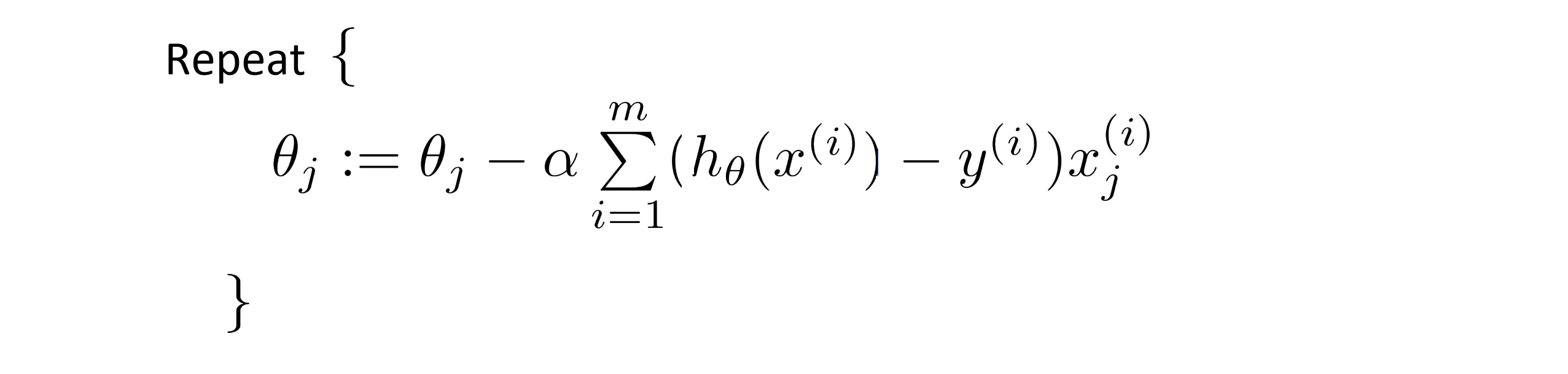
如果你把这个过程和我们之前的线性回归模型的梯度下降法进行比较的话，你会惊讶地发现，他们是一样的，唯一不同的就是我们的假设函数 hθ(x) 的表达形式发生了改变。

之前我们谈到过如何用图像的形式辅助我们观察线性回归的梯度下降法是否收敛，其实对于逻辑回归我们也能运用相似的方法辅助我们判断。并且之前提到的参数向量化的优化手段也能运用于此。

代码实现

算法的思路在上面也说的很清楚了，下面展示cpp的代码实现，供大家参考学习：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
double ans[11000];
double temp[11000], h[11000];
double x[11000][1100], y[11000];
const double Alpha = 3 * 1e-4;
const double e = 2.7182818284;
void read() {
    printf("请输入样本大小:\n");
    scanf("%d", &n);

    printf("请输入特征值的个数:\n");
    scanf("%d", &m);

    for(int i = 1; i <= n; i++) x[i][0] = 1;

    printf("请依次输入m个特征值xi和结果y(0 or 1):\n");
    for(int i = 1; i <=n; i++) { 
        for(int j = 1; j <= m; j++) {
            scanf("%lf", &x[i][j]);
        }
        scanf("%lf", &y[i]);
    }
    return;
}

void work() {
    memset(ans, 0, sizeof(ans));
    double delta = 1;
    int num;
    printf("请输入下降次数:\n"); 
    scanf("%d", &num);

    for(int o = 1; o <= num; o++) {
        for(int i = 0; i <= m; i++) temp[i] = ans[i];
        //==========================================
        for(int i = 1; i <= n; i++) {
            h[i] = 0;
            for(int j = 0; j <= m; j++)
            {
                h[i] += x[i][j] * ans[j];
            }
            h[i] = 1 / (1 + pow(e, -h[i]));
            h[i] -= y[i];
        }
        //==========================================
        for(int i = 0; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                temp[i] = temp[i] - (Alpha / (double)m) * h[j] * x[j][i];
            }
        }
        //==========================================
        for(int i = 0; i <= m; i++) ans[i] = temp[i];
    }
    return ;
}

void write() {
    printf("决策边界为：");
    printf("y = %0.1lf", ans[0]);
    for(int i = 1; i <= m; i++) {
        if(ans[i] >= 0)printf(" + %0.1f * x%d", ans[i], i);
        else printf(" - %0.1f * x%d", -ans[i], i);
    }
    printf("\n");
}
int main() {

    read();
    work();
    write();
    return 0;
}  

其效果也是非常不错的：

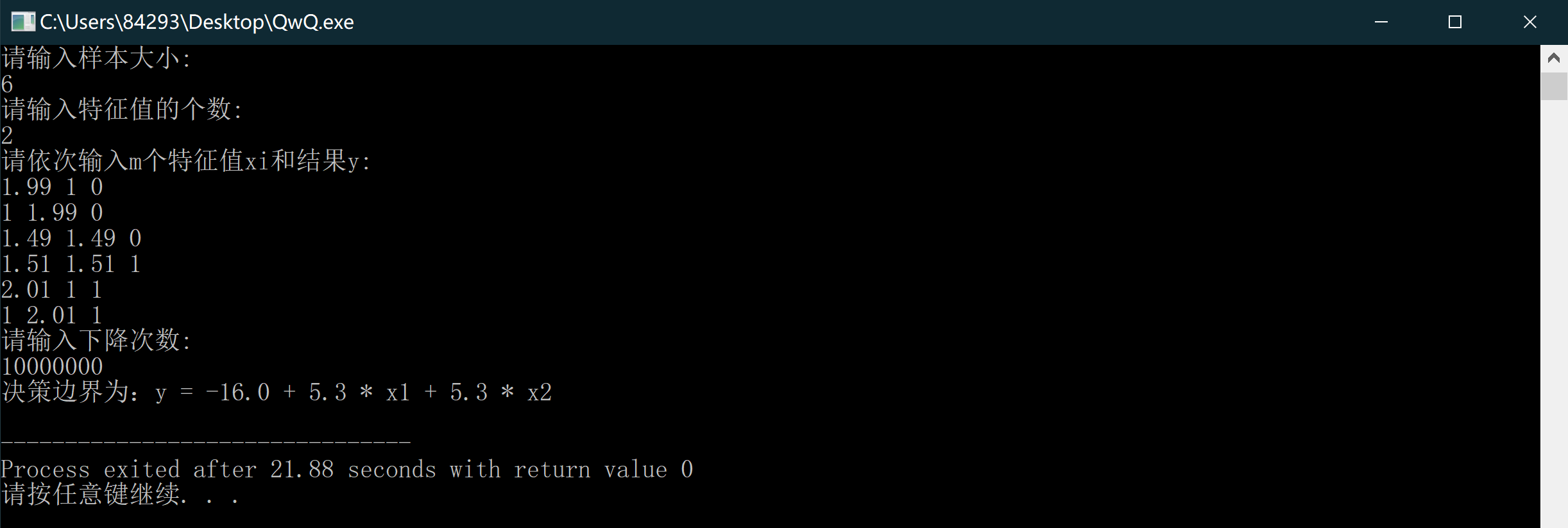
结语

通过这篇BLOG，相信你已经掌握了逻辑回归模型的解决办法，快去尝试一下吧！最后希望你喜欢这篇BLOG！